Girl students constitute 10% of I year and 5% of II year at Roorkee University. During summer holidays 70% of the I year and 30% of II year students are given a project. The chance that I year girl student is on duty in a randomly selected day is
317
1417
310
710
The correct Answer is:B
To solve the problem step by step, we need to follow the given information and apply the concepts of probability.
Step 1: Define the Variables
Let:
- G1 = event that a student is a girl from the first year.
- G2 = event that a student is a girl from the second year.
- P1 = event that a student is given a project in the first year.
- P2 = event that a student is given a project in the second year.
Step 2: Calculate the Probabilities
From the problem, we know:
- The probability that a student is a girl in the first year, P(G1)=10%=10100=0.1.
- The probability that a student is a girl in the second year, P(G2)=5%=5100=0.05.
- The probability that a first-year student is given a project, P(P1)=70%=70100=0.7.
- The probability that a second-year student is given a project, P(P2)=30%=30100=0.3.
Step 3: Calculate the Joint Probabilities
We need to find the probability that a randomly selected girl student is on duty. This can be calculated using the law of total probability.
1. The probability that a girl student from the first year is on duty:
P(G1∩P1)=P(G1)×P(P1)=0.1×0.7=0.07
2. The probability that a girl student from the second year is on duty:
P(G2∩P2)=P(G2)×P(P2)=0.05×0.3=0.015
Step 4: Total Probability of a Girl Student Being on Duty
Now, we can find the total probability that a randomly selected student is a girl and is on duty:
P(G∩P)=P(G1∩P1)+P(G2∩P2)=0.07+0.015=0.085
Step 5: Calculate the Total Probability of Being on Duty
Next, we need to find the total probability of being on duty, which includes both first-year and second-year students:
P(P)=P(G1∩P1)+P(G2∩P2)+P(not G1∩P1)+P(not G2∩P2)
However, since we are only interested in the girls, we can directly use the probabilities we calculated.
Step 6: Final Probability Calculation
Now, we can find the probability that a randomly selected student who is on duty is a girl:
P(G|P)=P(G∩P)P(P)=0.0850.085+(1−0.1)×0.7+(1−0.05)×0.3
Calculating the denominator:
- The probability of a boy from the first year on duty: 0.9×0.7=0.63
- The probability of a boy from the second year on duty: 0.95×0.3=0.285
Thus:
P(P)=0.085+0.63+0.285=1
So:
P(G|P)=0.0851=0.085
Conclusion
The chance that a first-year girl student is on duty on a randomly selected day is 0.085 or 8.5%.
Let:
- G1 = event that a student is a girl from the first year.
- G2 = event that a student is a girl from the second year.
- P1 = event that a student is given a project in the first year.
- P2 = event that a student is given a project in the second year.
From the problem, we know:
- The probability that a student is a girl in the first year, P(G1)=10%=10100=0.1.
- The probability that a student is a girl in the second year, P(G2)=5%=5100=0.05.
- The probability that a first-year student is given a project, P(P1)=70%=70100=0.7.
- The probability that a second-year student is given a project, P(P2)=30%=30100=0.3.
We need to find the probability that a randomly selected girl student is on duty. This can be calculated using the law of total probability.
P(G1∩P1)=P(G1)×P(P1)=0.1×0.7=0.07
P(G2∩P2)=P(G2)×P(P2)=0.05×0.3=0.015
Now, we can find the total probability that a randomly selected student is a girl and is on duty:
P(G∩P)=P(G1∩P1)+P(G2∩P2)=0.07+0.015=0.085
Next, we need to find the total probability of being on duty, which includes both first-year and second-year students:
P(P)=P(G1∩P1)+P(G2∩P2)+P(not G1∩P1)+P(not G2∩P2)
Now, we can find the probability that a randomly selected student who is on duty is a girl:
P(G|P)=P(G∩P)P(P)=0.0850.085+(1−0.1)×0.7+(1−0.05)×0.3
Calculating the denominator:
- The probability of a boy from the first year on duty: 0.9×0.7=0.63
- The probability of a boy from the second year on duty: 0.95×0.3=0.285
P(P)=0.085+0.63+0.285=1
So:
P(G|P)=0.0851=0.085
The chance that a first-year girl student is on duty on a randomly selected day is 0.085 or 8.5%.
Topper's Solved these Questions
- PROBABILITY -2BOOK - DISHA PUBLICATIONCHAPTER - PROBABILITY -2EXERCISE - EXERCISE - 1 : CONCEPT BUILDER
60 Videos
- PRINCIPLE OF MATHEMATICAL INDUCTIONBOOK - DISHA PUBLICATIONCHAPTER - PRINCIPLE OF MATHEMATICAL INDUCTIONEXERCISE - Exercise-2 Concept Applicator
20 Videos
- PROBABILITY-1BOOK - DISHA PUBLICATIONCHAPTER - PROBABILITY-1EXERCISE - EXERCISE-1 : CONCEPT BUILDER
180 Videos
Similar Questions
Of the students in a school, it is known that 30% have 100% attendance and 70% students are irregular. Previous year results report that 70% of all students who have 100% attendance attain A grade and 10% irregular students attain A grade in their annual examination. At the end of the year, one student is chosen at random from the school and he was found to have an A grade. What is the probability that the student has 100% attendance ? Is regularity required only in school ? Justify your answer.
View Solution
If 25% of the studetns in university-2 in the year 2010 were females, what was the number of male students in the university same year ?
View Solution
Knowledge Check
In a school 70% of the students are girls.The number of boys are 510.Then the total number of students in the school is:
A850B1700C1830D1900In a school 70% of the students are girls. The number of boys are 510. Then the total number of students in the school is
A850B1700C830D1900The given Bar graph present the number of students from Science and Arts streams from a school in different years
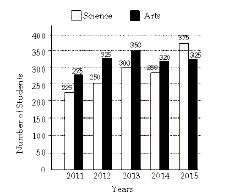
In which year the number of arts students is 30% more than that of science?A2013B2014C2012D2011
70% of the students in a school are boys and the number of girls is 504 find the number of boys in the school
View SolutionThe Cl on Rs. 5000 for 3 years at 8% for first year, 10% for second year and 12% for third year will be :
View SolutionThe Cl on Rs. 5000 for 3 years at 8% for first year, 10% for second year and 12% for third year will be :
View SolutionThe value of a machine is 6,250. It decreases by 10% during the first year, 20% during the second year and 30% during the third year. What will be the value of the machine after 3 years?
View SolutionIn a school there are 40% science students and the remaining 60% are arts students. It is known that 5% of the science students are girls and 10% of the arts students are girls. One student selected at random is a girl. What is the probability that she is an arts student?
View Solution
