Question

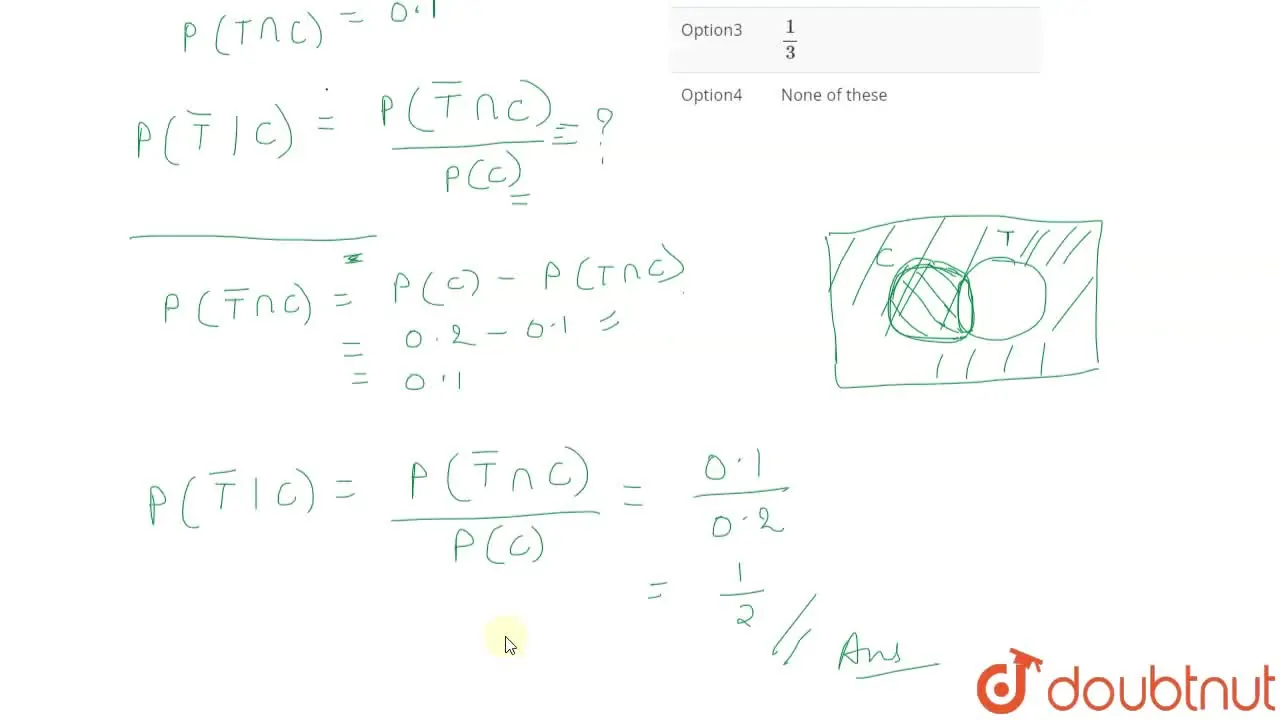
In a class 30% students like tea, 20% like coffee and 10% like both tea and coffee. A student is selected at random then what is the probability that he does not like tea if it is known that he likes coffee?

Options

A. `1/2`
B. `3/4`
C. `1/3`
D. None of these

Answer

A

Explanation

To solve the problem step by step, we will use the principles of probability and conditional probability.

Step 1: Define the events
Let:
- \( T \): the event that a student likes tea.
- \( C \): the event that a student likes coffee.

From the problem, we know:
- \( P(T) = 0.3 \) (30% like tea)
- \( P(C) = 0.2 \) (20% like coffee)
- \( P(T \cap C) = 0.1 \) (10% like both tea and coffee)

Step 2: Find the probability of liking coffee but not tea
We need to find the probability that a student does not like tea given that they like coffee. This is represented as \( P(T^c | C) \), where \( T^c \) is the complement of \( T \) (not liking tea).

Using the formula for conditional probability:
\( P(T^c | C) = \frac{P(T^c \cap C)}{P(C)} \)

Step 3: Calculate \( P(T^c \cap C) \)
To find \( P(T^c \cap C) \), we can use the relationship:
\( P(T^c \cap C) = P(C) - P(T \cap C) \)
Substituting the known values:
\( P(T^c \cap C) = P(C) - P(T \cap C) = 0.2 - 0.1 = 0.1 \)

Step 4: Calculate \( P(T^c | C) \)
Now we can substitute \( P(T^c \cap C) \) and \( P(C) \) into the conditional probability formula:
\( P(T^c | C) = \frac{P(T^c \cap C)}{P(C)} = \frac{0.1}{0.2} = 0.5 \)

Conclusion
The probability that a student does not like tea given that they like coffee is \( 0.5 \) or \( \frac{1}{2} \).