There are 10 bags B1,B2,B3,...,B10,which contain 21, 22? 30 different articles respectively. The total number of ways to bring out 10 articles from a bag is
The correct Answer is:C
To solve the problem of determining the total number of ways to bring out 10 articles from 10 bags (B1, B2, ..., B10) containing 21, 22, ..., 30 different articles respectively, we can follow these steps:
1. Identify the number of articles in each bag:
- Bag B1 contains 21 articles.
- Bag B2 contains 22 articles.
- Bag B3 contains 23 articles.
- Bag B4 contains 24 articles.
- Bag B5 contains 25 articles.
- Bag B6 contains 26 articles.
- Bag B7 contains 27 articles.
- Bag B8 contains 28 articles.
- Bag B9 contains 29 articles.
- Bag B10 contains 30 articles.
2. Determine the combinations for selecting articles from each bag:
- The number of ways to choose 10 articles from each bag can be represented using the binomial coefficient (nCr), where n is the number of articles in the bag and r is the number of articles we want to choose.
- Therefore, the total ways to choose 10 articles from each bag can be expressed as:
- From B1: (2110)
- From B2: (2210)
- From B3: (2310)
- From B4: (2410)
- From B5: (2510)
- From B6: (2610)
- From B7: (2710)
- From B8: (2810)
- From B9: (2910)
- From B10: (3010)
3. Sum the combinations:
- The total number of ways to bring out 10 articles from any of the bags is the sum of the combinations from each bag:
Total Ways=(2110)+(2210)+(2310)+(2410)+(2510)+(2610)+(2710)+(2810)+(2910)+(3010)
4. Use the identity for binomial coefficients:
- We can use the identity that relates binomial coefficients:
(nr)=(n−1r)+(n−1r−1)
- This allows us to express the sums in a different form, but for our purpose, we can directly calculate the sum as stated.
5. Calculate the individual terms:
- Calculate each binomial coefficient using a calculator or software that can handle combinatorial calculations.
6. Final Calculation:
- Add all the calculated values together to get the final total number of ways to select 10 articles from the bags.
- Bag B1 contains 21 articles.
- Bag B2 contains 22 articles.
- Bag B3 contains 23 articles.
- Bag B4 contains 24 articles.
- Bag B5 contains 25 articles.
- Bag B6 contains 26 articles.
- Bag B7 contains 27 articles.
- Bag B8 contains 28 articles.
- Bag B9 contains 29 articles.
- Bag B10 contains 30 articles.
- The number of ways to choose 10 articles from each bag can be represented using the binomial coefficient (nCr), where n is the number of articles in the bag and r is the number of articles we want to choose.
- Therefore, the total ways to choose 10 articles from each bag can be expressed as:
- From B1: (2110)
- From B2: (2210)
- From B3: (2310)
- From B4: (2410)
- From B5: (2510)
- From B6: (2610)
- From B7: (2710)
- From B8: (2810)
- From B9: (2910)
- From B10: (3010)
- The total number of ways to bring out 10 articles from any of the bags is the sum of the combinations from each bag:
Total Ways=(2110)+(2210)+(2310)+(2410)+(2510)+(2610)+(2710)+(2810)+(2910)+(3010)
- We can use the identity that relates binomial coefficients:
(nr)=(n−1r)+(n−1r−1)
- This allows us to express the sums in a different form, but for our purpose, we can directly calculate the sum as stated.
- Calculate each binomial coefficient using a calculator or software that can handle combinatorial calculations.
- Add all the calculated values together to get the final total number of ways to select 10 articles from the bags.
Topper's Solved these Questions
Similar Questions
There are 10 bags B1,B2,B3,......,B10 which contain 21,22,....,30 different articles respectively. The total number of ways to bring out 10 articles J'from any one bag is
View SolutionThere are two bags each containing 10 books all haing different titles but of the same size A student draws out any number of books from first bag as well as from the second bag. Find the probability that the difference between the number of books drawn from the two bags does not exceed two .
View Solution
Knowledge Check
There are 31 in a bag is which 10 are identical, then then the number of ways of choosing 10 objects from bag is
A220B220−1C220−1D221A bag contains 30 tokens numbered serially from 0 to 29. The number of ways of choosing 3 tokens from the bag, such that the sum on them is 30, is
A56B44C75D81The Table shows the number of articles sold by six different sellers (A, B, C, D, E and F) to two different shopkeepers P and Q. Some articles are purchased by other sellers also. Total articles purchased by shopkeepers P and Q is 300 and 500 respectively.
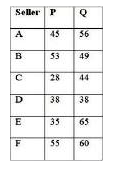
Total number of articles sold by seller C to shopkeeper Q is what percent of total number of articles sold by seller F to shopkeeper P?A0.75B0.84C0.78D0.8
If the set A contains 7 elements and the set B contains 10 elements, then the number of one-one functions from A to B is
View SolutionThe number of zeros at the end of 510! is a10−1b then a+b is
View SolutionThe profit percentage on the three articles A, B and C is 10%, 20% and 25% respectively and the ratio of the cost prices is 1:2:4. Also the ratio of number of articles sold of A, B and C is 2: 5: 2 then the overall profit percentage is
View SolutionThere are three bags B1,B2,B3,B1 contians 5 red and 5 green balls. B2 contains 3 red and 5 green balls and B3 contains 5 red and 3 green balls, bags B1,B2 and B3 have probabilities 3/10, 3/10, and 4/10
respectively of bieng chosen. A bag is selected at randon and a ball is randomly chosen from the bag. then which of the following options is/are correct?
View SolutionThere are three bags B1,B2andB3. The bag B1 contains 5 red and 5 green balls, B2 contains 3 red 5 green balls, and B3 contains 5 red and 3 green balls. Bags B1,B2andB3 have probabilities (3)/(10),(3)/(10) and (4)/(10) respectively of being chosen. A bag is selected at random and a ball is chosen at random form the bag. then which of the following options is/are correct ?
View Solution
