Having started from the same pint and at the same time, two runners A and B are running around a circular track of length 300m in opposite directions with speeds of 5m/s and 8m/s respectively. If they exchange their speeds after meeting for the first time, who will reach the starting point first?
The correct Answer is:A
To solve the problem step by step, let's break down the movements of runners A and B.
Step 1: Calculate the time taken for A and B to meet for the first time.
Formula: When two objects move towards each other, their relative speed is the sum of their speeds.
- Speed of A = 5 m/s
- Speed of B = 8 m/s
- Relative speed = Speed of A + Speed of B = 5 m/s + 8 m/s = 13 m/s
Distance: Since they are running on a circular track of length 300 m, they will meet when they have covered this distance.
Time to meet:
Time=DistanceRelative Speed=300 m13 m/s≈23.08 seconds
Step 2: Calculate the distance each runner covers before they meet.
Distance covered by A:
Distance=Speed×Time=5 m/s×23.08 s≈115.38 m
Distance covered by B:
Distance=Speed×Time=8 m/s×23.08 s≈184.62 m
Step 3: Determine the remaining distance each runner has to cover to reach the starting point after meeting.
Remaining distance for A:
- Total distance of the track = 300 m
- Distance covered by A = 115.38 m
Remaining distance for A=300 m−115.38 m≈184.62 m
Remaining distance for B:
- Total distance of the track = 300 m
- Distance covered by B = 184.62 m
Remaining distance for B=300 m−184.62 m≈115.38 m
Step 4: Calculate the time taken for each runner to reach the starting point after they exchange speeds.
New speeds after exchange:
- Speed of A after exchange = 8 m/s
- Speed of B after exchange = 5 m/s
Time taken by A to reach starting point:
Time=Remaining DistanceSpeed=184.62 m8 m/s≈23.08 seconds
Time taken by B to reach starting point:
Time=Remaining DistanceSpeed=115.38 m5 m/s≈23.08 seconds
Step 5: Compare the total time taken by both runners to reach the starting point.
- Total time for A = Time to meet + Time to reach starting point = 23.08 s + 23.08 s = 46.16 s
- Total time for B = Time to meet + Time to reach starting point = 23.08 s + 23.08 s = 46.16 s
Conclusion:
Both runners A and B will reach the starting point at the same time.
---
- Speed of B = 8 m/s
- Relative speed = Speed of A + Speed of B = 5 m/s + 8 m/s = 13 m/s
Time=DistanceRelative Speed=300 m13 m/s≈23.08 seconds
Distance=Speed×Time=5 m/s×23.08 s≈115.38 m
Distance=Speed×Time=8 m/s×23.08 s≈184.62 m
- Total distance of the track = 300 m
- Distance covered by A = 115.38 m
Remaining distance for A=300 m−115.38 m≈184.62 m
- Total distance of the track = 300 m
- Distance covered by B = 184.62 m
Remaining distance for B=300 m−184.62 m≈115.38 m
- Speed of A after exchange = 8 m/s
- Speed of B after exchange = 5 m/s
Time=Remaining DistanceSpeed=184.62 m8 m/s≈23.08 seconds
Time=Remaining DistanceSpeed=115.38 m5 m/s≈23.08 seconds
- Total time for B = Time to meet + Time to reach starting point = 23.08 s + 23.08 s = 46.16 s
Both runners A and B will reach the starting point at the same time.
Topper's Solved these Questions
- TIME, SPEED AND DISTANCEBook:ARIHANT SSCChapter:TIME, SPEED AND DISTANCEExercise:EXERCISE LEVEL 2
Explore 75 Videos
- TIME, SPEED AND DISTANCEBook:ARIHANT SSCChapter:TIME, SPEED AND DISTANCEExercise:SPEED TEST (TSD)
Explore 10 Videos
- TIME, SPEED AND DISTANCEBook:ARIHANT SSCChapter:TIME, SPEED AND DISTANCEExercise:INTRODUCTORY EXERCISE(9.1 )
Explore 3 Videos
- TIME AND WORKBook:ARIHANT SSCChapter:TIME AND WORKExercise:Final Round
Explore 15 Videos
- TRIGONOMETRYBook:ARIHANT SSCChapter:TRIGONOMETRYExercise:EXERCISE(LEVEL - 1)
Explore 35 Videos
Similar Questions
Two trains are moving in opposite directions withs peed s of 4m/s and 8m/s,respectively.Find their relative speed.
View SolutionA, B and C are running on a circular track of radius 63 m. B and C run in the opposite direction of A. If the speed of A, B and C is 30, 25 and 14 m/minutes respectively then find when will they meet together first time and when will they together meet at the starting point?
View Solution
Knowledge Check
Two cyclists start on a circular track from a given point but in opposite directions with speeds of 7 m/sec and 8 m/sec respectively. If the circumference of the circle is 300 metres, after what time will they meet at the starting point ?
A100 secB20 secC300 secD200 secA circular running path is 726 metres in circumference. Two men start from the same point and walk in opposite directions at 3.75 km/h and 4.5 km/h, respectively. When will they meet for the first time ?
AAfter 5.5 minBAfter 6.0 minCAfter 5.28 minDAfter 4.9 min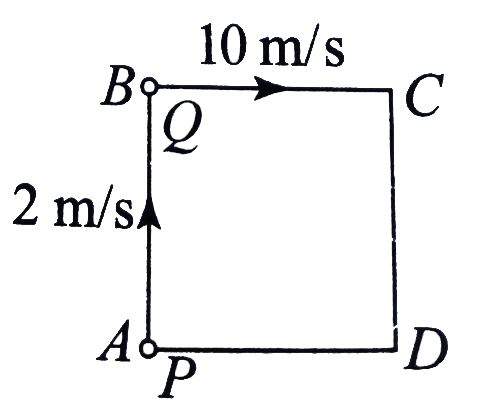
Two men P & Q are standing at corners A & B of square ABCD of side 8m. They start moving along the track with constant speed 2ms and 10ms respectively. Find the time when they will meet for the first timeA2 secB3 secC1 secD6 sec
Three cyclists with respective speeds of 8 m/sec, 10 m/sec and 20 m/sec are cycling arounda circular track of length 120 metres. If they are cycling in the same direction, after how many seconds do all the three meet for the first time at the starting point?
View SolutionTwo trains of lengths 75 m and 95 m are moving in the same direction at 9m/s and 8m/s, respectively. Find the time taken by the faster train to cross the slower train.
View SolutionArjun and Bhishma are running on a circular track of length 600 m (i.e., circumference of the track). Speed of Arjun is 30 m/s and that of Bhishma is 20 m/s. They start from the same point at the same time in the same direction. When will they meet again for the first time?
View SolutionP and Q start running on the circular track in opposite directions they starts from a point A and meet for the first second and third time at B,C and A respectively. what is the ratio of speeds of P and Q?
View SolutionArjun and Bishma are runing on a circular track of length 600 m (i.e,circumfrence of the track is 600m).Speed of A rjun is 75m/s and that of Bhishma is 45 m/s they start running from the same point at the same time the same direction. When will they meet again for the first time?
View Solution
