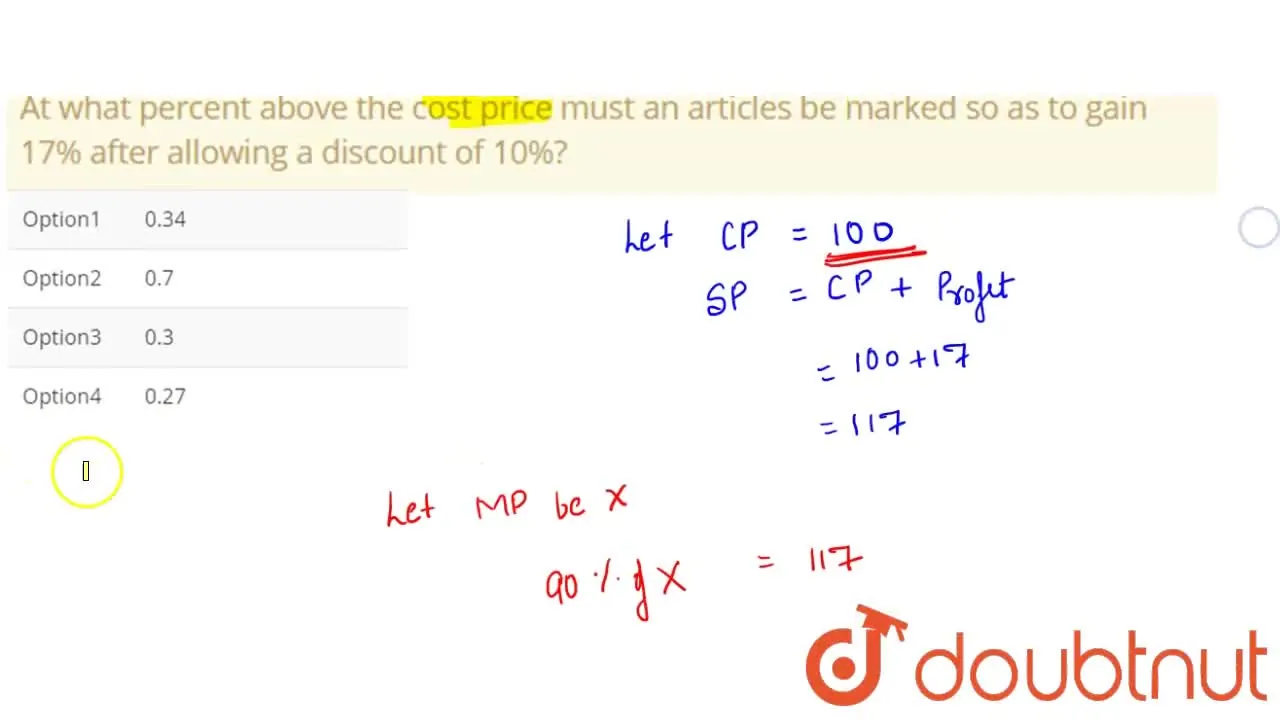
At what percent above the cost price must an articles be marked so as to gain 17% after allowing a discount of 10%?
0.34
0.7
0.3
0.27
The correct Answer is:C
Step by step video, text & image solution for At what percent above the cost price must an articles be marked so as to gain 17% after allowing a discount of 10%? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Related Playlists
- BOOK - ARIHANT SSCCHAPTER - PROFIT, LOSS AND DISCOUNTEXERCISE - EXERCISE (LEVEL 1)70videos
PROFIT, LOSS AND DISCOUNT
- BOOK - ARIHANT SSCCHAPTER - PROFIT, LOSS AND DISCOUNTEXERCISE - EXERCISE (LEVEL 2)45videos
PROFIT, LOSS AND DISCOUNT
- BOOK - ARIHANT SSCCHAPTER - PROFIT, LOSS AND DISCOUNTEXERCISE - INTRODUCTORY EXERCISE 6 .15videos
PROFIT, LOSS AND DISCOUNT
- BOOK - ARIHANT SSCCHAPTER - PROFIT AND LOSSEXERCISE - Higher Skill Level Questions16videos
PROFIT AND LOSS
- BOOK - ARIHANT SSCCHAPTER - QUADRATIC EQUATIONSEXERCISE - Exercise Higher Skill Level questions19videos
QUADRATIC EQUATIONS
Similar Questions
At what per cent above the cost price must an articles be marked, so as to gain 17% after allowing a discount of 10%?
View SolutionAt what percentage above the cost price must an article be marked so as to gain 38% after allowing a customer a discount of 8% on the marked price?
View SolutionAt what percentage above the cost price must an article be marked so as to gain 33% after allowing a customer a discount of 5% ?
View SolutionHow much per cent above the cost price should a shopkeeper mark his goods so that after allowing a discount of 10% on the marked price, he gains 8%
View SolutionHow much per cent above the cost price should a shopkeeper mark his goods so that after allowing a discount of 10% on the marked price, he gains 8%?
View SolutionAt what percent above the cost price must a shopkeeper mark his goods so that he gains 20% even after giving a discount of 10% on the marked price? 25% b. 30% c. 3313% d. 3712%
View SolutionHow much percent above the cost price should a shopkeeper mark his goods so that after allowing a discount of 25% on the marked price, he gains 20%?
View SolutionAt what percent above the cost price must a shopkeeper mark his goods so that he gains 20% even after giving a discount of 10% on the marked price? 25% b. 30% c. 3313% d. 3712%
View SolutionAt what per cent above the cost price, must a shop-keeper marks his goods so that he gains 20% even after giving a discount of 10% on the marked price?
View SolutionHow much per cent more than the cost price should a shopkeeper marks his goods so that after allowing a discount of 20% on the marked price, he gains 10%?
View Solution