If A= {(x,y) : y = ex,x∈R} and B = { (x,y) : y = e−x,x∈R } then n (A ∩ B ) is Solution in Tamil
Infinity
0
1
2
The correct Answer is:C
Step by step video, text & image solution for If A= {(x,y) : y = e^(x), x in R } and B = { (x,y) : y = e^(-x), x in R } then n (A cap B ) is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SETS, RELATIONS AND FUNCTIONSBook:FULL MARKSChapter:SETS, RELATIONS AND FUNCTIONSExercise:Exercise -1.4
Explore 4 Videos
- SAMPLEPAPER - 15 (UNSOLVED)Book:FULL MARKSChapter:SAMPLEPAPER - 15 (UNSOLVED)Exercise:Part - IV (IV. Answer all the questions.)
Explore 7 Videos
- SOLVED PAPER 10Book:FULL MARKSChapter:SOLVED PAPER 10Exercise:PART-IV
Explore 8 Videos
Similar Questions
Graph the functions f (x) = x3 and g(x) = 3√x on the same co-ordinate plane. Find fog and graph it on the plane as well. Explain your results.
View SolutionIf αandβ are the roots of the quadratic equation x2+√2x+3=0 form a quadratic equation with roots1αand1β
View SolutionGraph the functions f(x)=x3andg(x)=3√x on the same coordinate plane. Find f o g and graph it on the plane as well. Explain your results.
View SolutionIf A={(x,y):y=e^(x),x in R} and B={(x,y):y=e^(-2x),x in R}, then
View SolutionIf A={(x, y):y=ex, x∈R}and B={(x,y):y=x,x∈R} , then write A∩B.
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
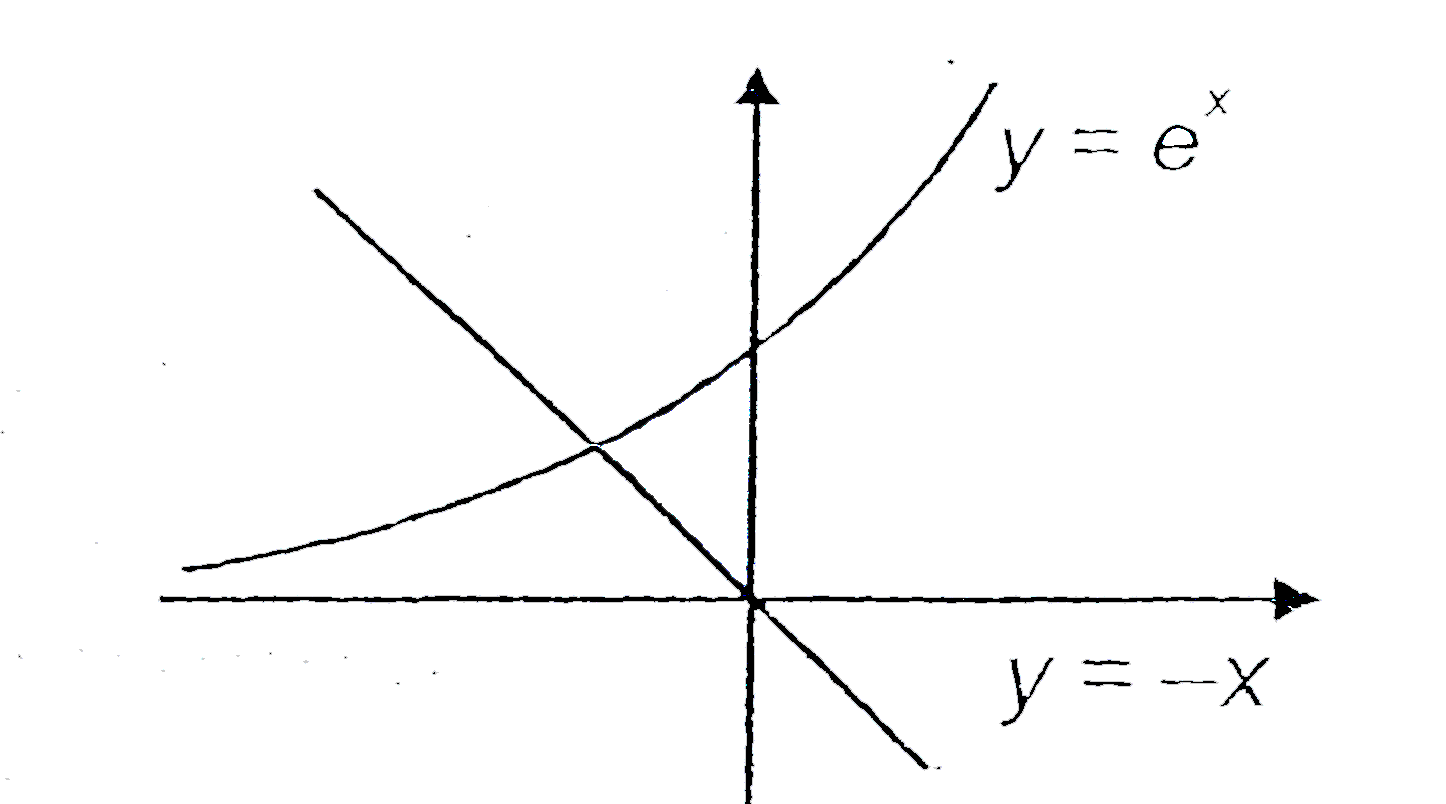
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A:{(x,y):y=√4−x2,x∈[−2,2]}
B={(x,y):y=|x|,x∈R}
Then n(A∩B)
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
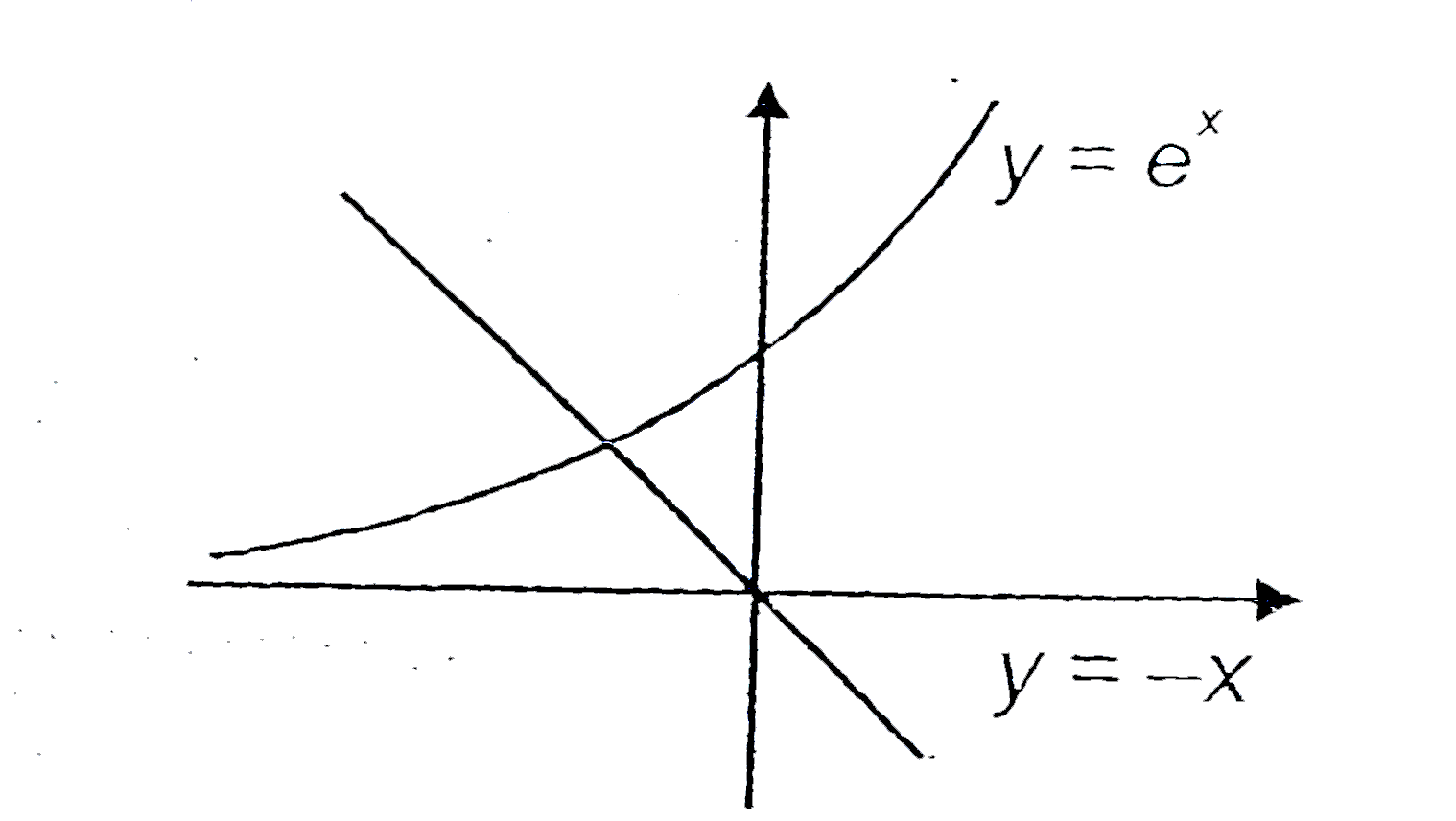
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):x2+y2≤2,x,y∈R}
B={{x,y):y≥x2,x,y∈R}
Then domain of A∩B is
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
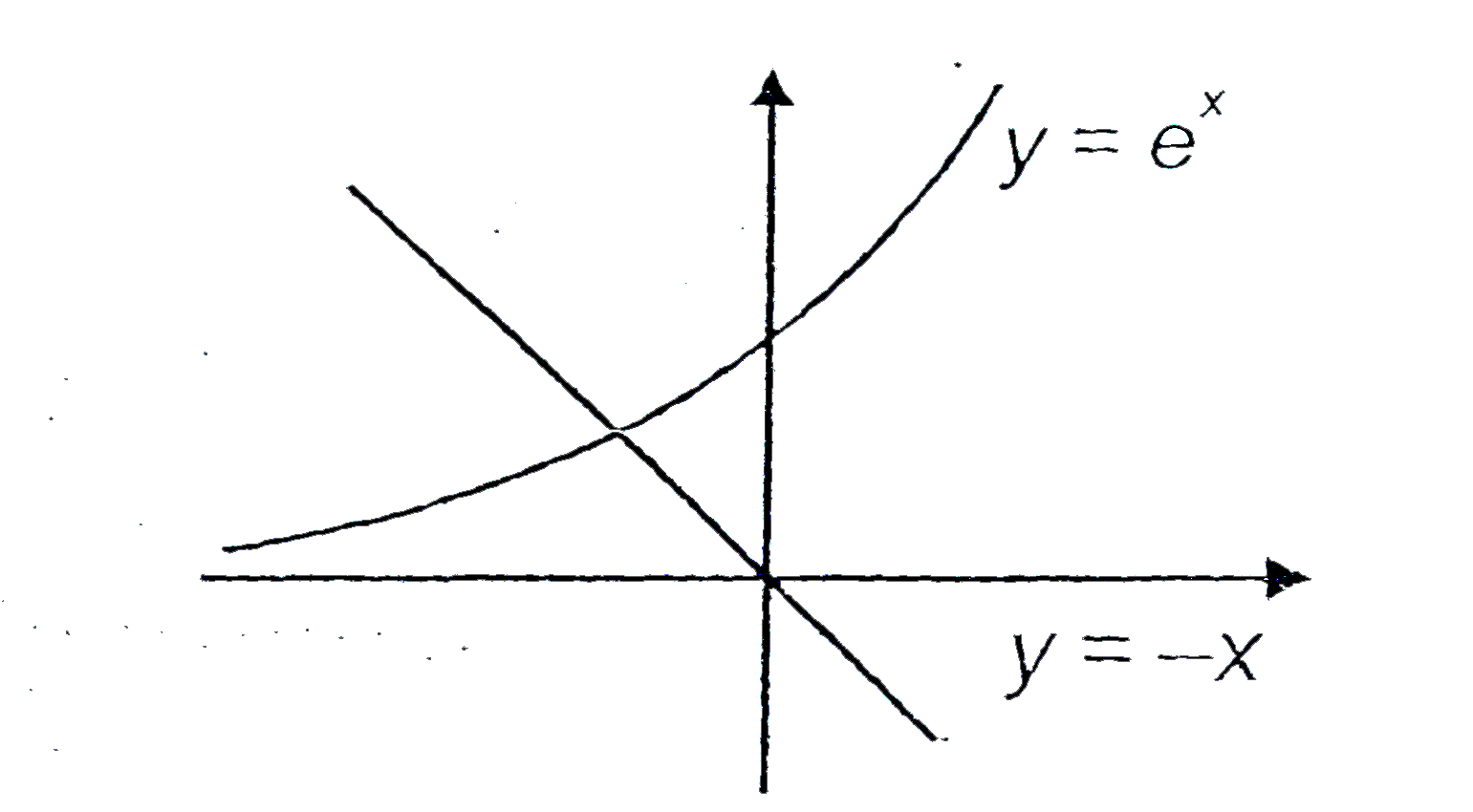
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):y=sinπx,x∈R}
B={(x,y):y=|In|x||,x∈R−{0}}
Then, n(A∩B)
View SolutionLet A={(x,y):y=ex,x∈R}B={(x,y),Y=e−x,x∈R}then
View SolutionIf A= {(x,y) : y = ex,x∈R} and B = { (x,y) : y = e−x,x∈R } then n (A ∩ B ) is
View SolutionA={(x,y):y:y=ex,x∈R},B={(x,y):y=e−x,x∈R} then
View SolutionA={(x,y):y=ex,x∈R},B={(x,y):y=x,x∈R} then
View SolutionLet A={(x,y)∣y=ex,x∈R}andB={(x,y)∣=e−x,x∈R}. Then
View SolutionIf A ={(x,y):y=ex,xεR} and B={(x,y):y=e−x,xεR) then n(A∩B) is _________
View SolutionLet A={(x,y): y=ex,x∈R } , B={(x,y): y= e−x,x∈R } . Then :
View SolutionLet A={(x,y : y=ex,x∈R} , B={(x,y): y=x, x ∈ R} . Then :
View Solution

