lines L1:ax+by+c=0 and L2:lx+my+n=0 intersect at the point P and make a angle θ between each other. find the equation of a line Ldifferent from L2 which passes through P and makes the same angle θ with L1
Since, the required line L passes through the intersection of L1=0 and L2=0
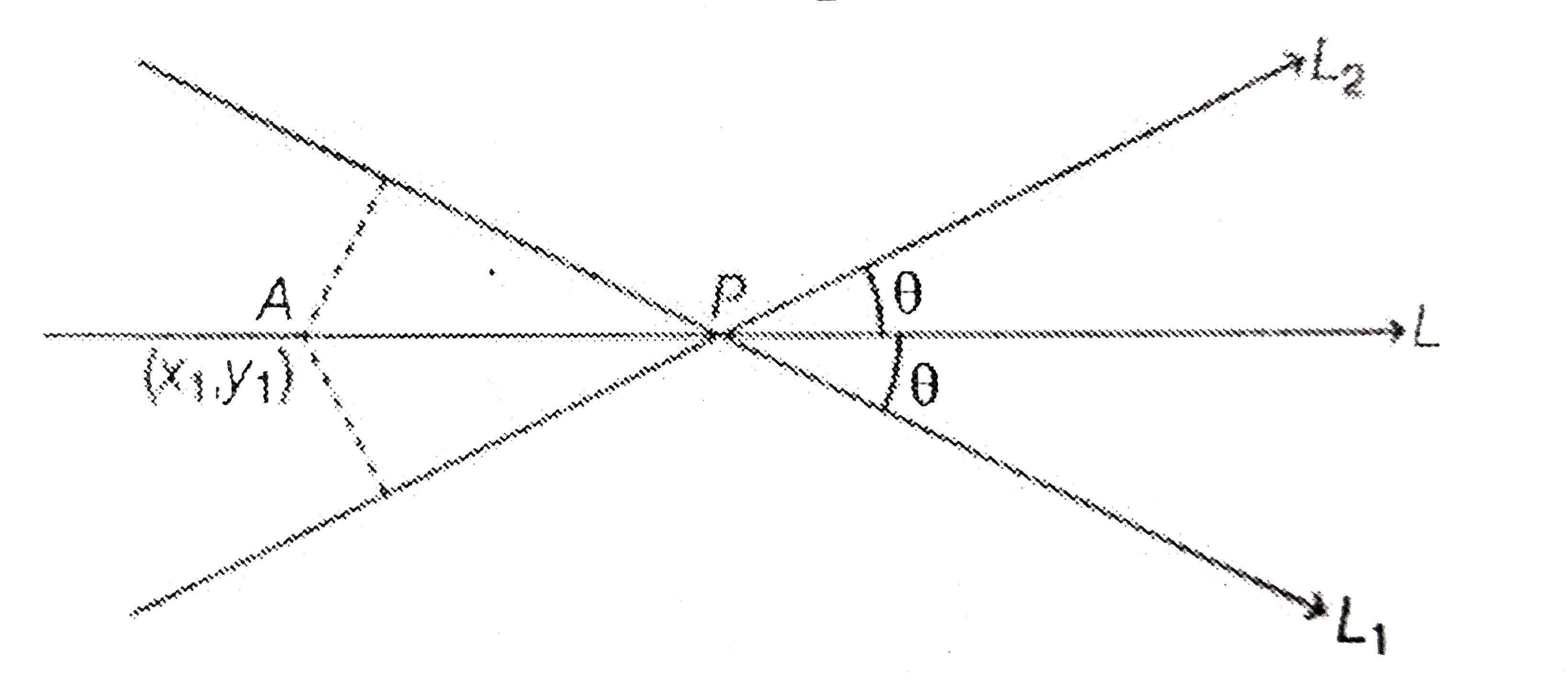
So, the equation of the required line L is
L1+λL2=0
i.e. (ax+by+c)+λ(lx+my+n)=0……(i)
where, λ is a parameter.
Since, L1 is the angle bisector of L=0 and L2=0.
∴ Any point A(x1,y1) on L1 is equidistant from L1=0 and L2=0
⇒|lx1+my1+n|√l2+m2
=|(ax1+by1+c)+λ(lx1+my1+n)|√(a+λl)2+(b+λm)2.......(ii)
But A(x1,y1) lies on L1. So, itmust satisfy the equation of L1, ie, ax1+by1+c1=0
On substituting ax1+by1+c=0 in Eq. (ii) , we get
|lx1+my1+n|√l2+m2=|0+λ(lx1+my1+n)|√(a+λl)2+(b+λm)2
⇒λ2(l2+m2)=(a+λl)2+(b+λm)2
∴λ=−(a2)+b22(al+bm)
On substituting the value of λ in Eq.(i), we get
(ax+by+c)−(a2+b22(al+bm)(lx+my+n)=0
⇒2(al+bm)(ax+by+c)−(a2+b2)(lx+my+n)=0
which is the required equation of line L.
Topper's Solved these Questions
- STRAIGHT LINE AND PAIR OF STRAIGHT LINESBOOK - IIT JEE PREVIOUS YEARCHAPTER - STRAIGHT LINE AND PAIR OF STRAIGHT LINESEXERCISE - AREA AND FAMILY OF CONCURRENT LINES (Objective Questions I) (Only one correct option)
7 Videos
- STRAIGHT LINE AND PAIR OF STRAIGHT LINESBOOK - IIT JEE PREVIOUS YEARCHAPTER - STRAIGHT LINE AND PAIR OF STRAIGHT LINESEXERCISE - AREA AND FAMILY OF CONCURRENT LINES (Objective Questions II) (Only or more than one correct option)
1 Videos
- STRAIGHT LINE AND PAIR OF STRAIGHT LINESBOOK - IIT JEE PREVIOUS YEARCHAPTER - STRAIGHT LINE AND PAIR OF STRAIGHT LINESEXERCISE - ANGLE BETWEEN STRAIGHT LINE AND EQUATION OF ANGLE BISECTOR (Fill in the Blanks)
1 Videos
- SOLVED PAPER 2019BOOK - IIT JEE PREVIOUS YEARCHAPTER - SOLVED PAPER 2019EXERCISE - Paper -2 section-3
4 Videos
- THEORY OF EQUATIONSBOOK - IIT JEE PREVIOUS YEARCHAPTER - THEORY OF EQUATIONSEXERCISE - SOME SPECIAL FORMS
18 Videos
Similar Questions
Lines L1=ax+by+c=0andL2=lx+my+n=0 intersect at the point P and make an anlge θ with each other. Find the equation of a line different from L2 with pass through P and makes the same anlge θ with L1.
View SolutionLines L1≡ax+by+c=0 and L2≡lx+my+n=0 intersect at the point P and make an angle θ with each other. Find the equation of a line different from L2 which passes through P and makes the same angle θ with L1.
View Solution
Knowledge Check
The direction cosines of the lines bisecting the angle between the line whose direction cosines are l1,m1,n1andl2,m2,n2 and the angle between these lines is θ, are
Al1+l22sin(θ2),m1+m22sin(θ2),n1+n22sin(θ2)Bl1+l22cos(θ2),m1+m22cos(θ2),n1+n22cos(θ2)Cl1−l22sin(θ2),m1−m22sin(θ2),n1−n22sin(θ2)Dl1−l22cos(θ2),m1−m22cos(θ2),n1−n22cos(θ2)If the length of the perpendicular to a line L from the origin is 8 and the perpendicular makes an angle of 60∘ with the X-axis then the equation of line L is
Ax+y√3=16Bx√3+y=16Cx-y√3+16=0Dnone of theseIf l,m,nandl',m',n' be the direction cosines of two lines which include an angle θ, then
Acosθ=ll'+mm'+nn'Bsinθ=ll'+mm'+nn'Ccosθ=mn'+m'n+nl'+n'l+lm'+l'mDsinθ=mn'+m'n+nl'+n'l+lm'+l'm
Lines, L1:x+√3y=2,andL2:ax+by=1 meet at P and enclose an angle of 45° between them. Line L3:y=√3x also passes through P then -
View SolutionIf L1andL2, are two lines belonging to family of lines (3+2λ)x+(4+3λ)y−7−5λ=0 (λ is parameter) such that it is at maximum and miimum distance from (2, 3), respectively, then theequation of lines passing through (1,2) and making equal angles with L1andL2 is/are
View Solution(i) Find the equation of line passing through (2,2) and makes an angle of 135∘ from positive direction of X-axis.
(ii) Find the equation of a line passing through the point (2,1) and makes an angle 'θ' from the positive direction of X-axis where cosθ=−13.
View SolutionLines, L1:x+√13y=2,andL2:ax+by=1, meet at P and enclose an angle of 45∘ betweenthem. Line L3:y=√13x, also passes through P then
View Solutionif line 2x+7y−1=0 intersect the lines L1:3x+4y+1=0andL2:6x+8y−3=0 in AandB respectively, then equation of line parallal to L1andL2 and passes through a point P such that AP:PB=2:1 (internally) is (P is on the line 2x+7y−1=0)
View Solution
