Let $f (x) lim_{n \to \infty} {[\frac{n^{n} (x + n) (x + \frac{n}{2}) ... (x + \frac{n}{n})}{n! (x^{2 + n^{2}}) (x^{2} + \frac{n^{2}}{4}) ... (x^{2} + \frac{n^{2}}{n^{2}})}]}^{\frac{x}{n}}$ ,for all x = 0 . Then

A

$f (\frac{1}{2}) \geq f (1)$

B

$f (\frac{1}{3}) \leq f (\frac{2}{3})$

C

$f' (2) \leq 0$

D

$\frac{f' (3)}{f (3)} \geq \frac{f' (2)}{f (2)}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B, C

Here,
$f (x) = lim_{n \to \infty} {[\frac{n^{n} (x + n) (x + \frac{n}{2}) ... (x + \frac{n}{n})}{n! (x^{2} + n^{2}) (x^{2} + \frac{n^{2}}{4}) ... (x^{2} + \frac{n^{2}}{n^{2}})}]}^{\frac{x}{n}}, x > 0$
Taking log on both sides, we get
$\log_{e} {f (x)} = lim_{n \to \infty} {\log [\frac{n^{n} (x + n) (x + \frac{n}{2}) ... (x + \frac{n}{n})}{n! (x^{2} + n^{2}) (x^{2} + \frac{n^{2}}{4}) ... (x^{2} + \frac{n^{2}}{n^{2}})}]}^{\frac{x}{n}}$
$= lim_{n \to \infty} \frac{x}{n} \cdot \log [\frac{\underset{r = 1}{\overset{n}{II}} (x + \frac{1}{r / n})}{\underset{r = 1}{\overset{n}{II}} (x^{2} + \frac{1}{{(r / n)}^{2}}) \underset{r = 1}{\overset{n}{II}} (r / n)}]$
$= x lim_{n \to \infty} \frac{1}{n} \underset{r = 1}{\sum^{n}} \log [\frac{x + \frac{n}{r}}{(x^{2} + \frac{n^{2}}{r^{2}}) \frac{r}{n}}]$
$= x lim_{n \to \infty} \frac{1}{n} \underset{r = 1}{\sum^{n}} \log (\frac{\frac{r}{n} \cdot x + 1}{\frac{r^{2}}{n^{2}} \cdot x^{2} + 1})$
Converting summation into definite integraton, we get
$\log_{e} {f (x)} = x \int_{0}^{1} \log (\frac{x t + 1}{x^{2} t^{2} + 1}) d t$
Put, t x = z
$\Rightarrow x d t = d z$
$∴ \log_{e} {f (x)} = x \int_{0}^{x} \log (\frac{1 + z}{1 + z^{2}}) \frac{d z}{x}$
$\Rightarrow \log_{e} {f (x)} = \int_{0}^{x} \log (\frac{1 + z}{1 + z^{2}}) d z$
Using Newton-Leibnitz formula, we get
$\frac{1}{f (x)} \cdot f' (x) = \log (\frac{1 + x}{1 + x^{2}})$ .....(i)
Here, at x = 1,
$\frac{f' (1)}{f' (1)} = \log (1) = 0$
$∴ f' (1) = 0$
Now, sign scheme of f'(x) is shown below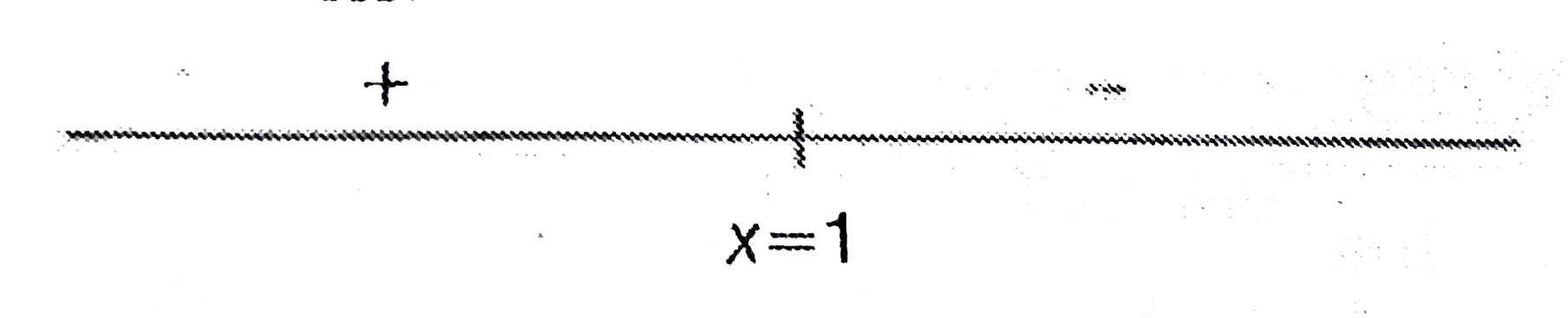
$∴$ At x = 1 , function attains maximum.
Since, f(x) increases on (0, 1).
$∴ f (1) > f (1 / 2)$
$∴$ Option (a) is incorrect.
$f (1 / 3) < f (2 / 3)$
$∴$ Option (b) is correct.
Also, $f' (x) < 0 when x > 1$
$\Rightarrow f' (2) < 0$
$∴$ Option (c ) is correct.
Also, $\frac{f' (x)}{f (x)} = \log (\frac{1 + x}{1 + x^{2}})$
$∴ \frac{f' (3)}{f (3)} - \frac{f' (2)}{f (3)} = \log (\frac{4}{10}) - \log (\frac{3}{5})$
$= \log (2 / 3) < 0$
$\Rightarrow \frac{f' (3)}{f (3)} < \frac{f' (2)}{f (2)}$
$∴$ Option (d) is incorrect.

Updated on:21/07/2023

|

Class 12 MATHS LIMITS AND DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

$lim n \to \infty n \sum k = 1 \frac{n}{n^{2} + k^{2} x^{2}}, x > 0$ is equal to
A $x {tan}^{- 1} (x)$
B ${tan}^{- 1} (x)$
C $\frac{{tan}^{- 1} (x)}{x}$
D $\frac{{tan}^{- 1} (x)}{x}$
Let $f (x) = lim n \to \infty \frac{{(2 sin x)}^{2 n}}{3^{n} - {(2 cos x)}^{2 n}}, n \in Z$ . Then
Aat $x = n \pm \frac{π}{6}$ , f(x) is discontinuous
B $f (\frac{π}{3}) = 1$
Cf(0)=0
Dall of the above
Consider $f (x) = lim n \to \infty \frac{x^{n} - {sin x}^{n}}{x^{n} + {sin x}^{n}}$ , for $x > 0, x \neq 1$ , f(1) =0, then
Af is continous at x=1
Bf has a finite discontinuity at x=1
Cf has an infinite or oscillatory discontinuity at x=1
Df has a removable type of discontinuity at x=1.

IIT JEE PREVIOUS YEAR-LIMIT,CONTINUITY AND DIFFERENTIABILITY -(Objective Questions II)

Home
Ask Doubt
Profile