PQRS is a cyclic quadrilateral and PQ is the diameter of circle . If ∠RPQ=38∘ , what is the value (in degrees) of ∠PSR ?
52
77
128
142
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Understand the properties of cyclic quadrilaterals
A cyclic quadrilateral is a quadrilateral whose vertices lie on a circle. One important property of cyclic quadrilaterals is that the sum of the opposite angles is equal to 180 degrees.
Step 2: Identify the given information
We are given that PQ is the diameter of the circle and that angle RPQ = 38 degrees. We need to find the value of angle PSR.
Step 3: Apply the inscribed angle theorem
Since PQ is the diameter of the circle, angle RPQ is an inscribed angle that subtends the arc PS. According to the inscribed angle theorem, any angle inscribed in a semicircle is a right angle. Therefore, angle RQP is 90 degrees.
Step 4: Find angle QRS
In triangle PQR, we know:
- Angle RPQ = 38 degrees
- Angle RQP = 90 degrees
Using the triangle sum property (the sum of angles in a triangle is 180 degrees), we can find angle QRS:
Angle QRS=180−Angle RPQ−Angle RQP
Angle QRS=180−38−90=52 degrees
Step 5: Use the property of cyclic quadrilaterals
Now, since PQRS is a cyclic quadrilateral, we can use the property that the sum of opposite angles is 180 degrees:
Angle PSR+Angle QRS=180
Substituting the known value of angle QRS:
Angle PSR+52=180
Step 6: Solve for angle PSR
Now we can solve for angle PSR:
Angle PSR=180−52=128 degrees
Final Answer
Thus, the value of angle PSR is 128 degrees.
---
A cyclic quadrilateral is a quadrilateral whose vertices lie on a circle. One important property of cyclic quadrilaterals is that the sum of the opposite angles is equal to 180 degrees.
We are given that PQ is the diameter of the circle and that angle RPQ = 38 degrees. We need to find the value of angle PSR.
Since PQ is the diameter of the circle, angle RPQ is an inscribed angle that subtends the arc PS. According to the inscribed angle theorem, any angle inscribed in a semicircle is a right angle. Therefore, angle RQP is 90 degrees.
In triangle PQR, we know:
- Angle RPQ = 38 degrees
- Angle RQP = 90 degrees
Angle QRS=180−Angle RPQ−Angle RQP
Angle QRS=180−38−90=52 degrees
Now, since PQRS is a cyclic quadrilateral, we can use the property that the sum of opposite angles is 180 degrees:
Angle PSR+Angle QRS=180
Substituting the known value of angle QRS:
Angle PSR+52=180
Now we can solve for angle PSR:
Angle PSR=180−52=128 degrees
Thus, the value of angle PSR is 128 degrees.
Similar Questions
Knowledge Check
PQRS is a cyclic quadrilateral and PQ is the diameter of circle . If ∠RPQ=38∘ , what is the value (in degrees) of ∠PSR ?
A52B77C128D142ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠CAB=48∘, then what is the value (in degrees) of ∠ADC?
A52B77C138D142PQRS is a cyclic quadrilateral. PR and QS intersect at T. If ∠SPR=40∘and∠PQS=80∘, then what is the value (in degrees) of ∠PSR?
A60B40C80D100
In the adjoining figure, ABCD is a cyclic quadrilateral whose side AB is the diameter of the circle . If ∠ADC=140∘ , then find the value of ∠BAC.

View SolutionTriangle PQR is inscribed in a circle such that P Q and R lie on the circumference. If PQ is the diameter of the circle and ∠PQR=40∘, then what is the value (in degree) of QPR?
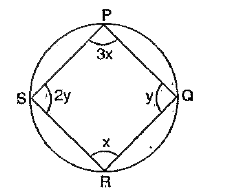
View SolutionPQRs is a cyclic quadrilateral. Find the measure of ∠Pand∠Q.
View SolutionTriangle PQR is inscribed in a circle such that P Q and R lie on the circumference. If PQ is the diameter of the circle and ∠PQR=40∘, then what is the value (in degree) of QPR?
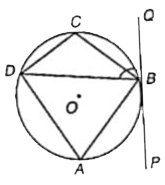
View SolutionABCD is a cyclic quadrilateral PQ is a tangent at B. If ∠DBQ=65∘, then ∠BCD is:
View Solution