A,O,B are three points on a line segment and C is a point not lying on AOB. If ∠AOC=40∘ and OX, OY are the internal and external bisectors of ∠AOC respectively, then ∠BOY is
70∘
80∘
72∘
68∘
The correct Answer is:A
Step by step video, text & image solution for A,O,B are three points on a line segment and C is a point not lying on AOB. If angleAOC = 40^(@) and OX, OY are the internal and external bisectors of angleAOC respectively, then angleBOY is by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Similar Questions
In the given figure, ray OC stands on a straight line AOB. Ray OD and ray OE are the bisectors of ∠AOC and ∠BOC respectively. Find the measure of ∠DOE.
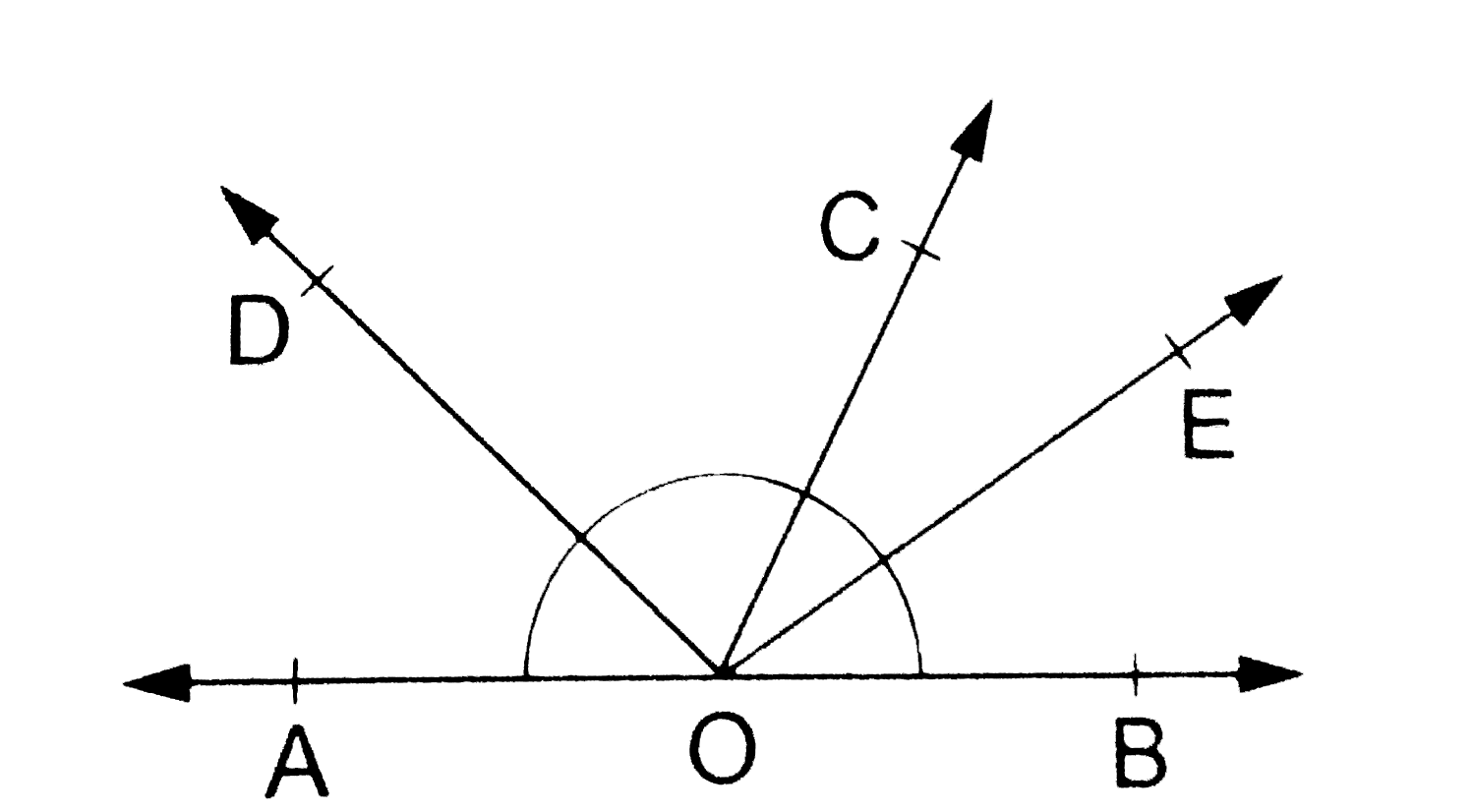 View Solution
View SolutionFind the coordinates of the point which divides the line segment joining (2,4) and (6,8) in the ratio1:3 internally and externally.
View Solution
Knowledge Check
- Question 1 - Select One
A,O,B are three points on a line segment and c is a point not lying on AOB if ∠AOC=40∘ and OX ,OY ar the internal and external bisections of ∠AOC respectively then ∠BOY is
A72∘B68∘C70∘D80∘ - Question 2 - Select One
If C and D are the points of internal and external division of line segment AB in the same ratio, then AC,AB, AD are in
AAPBGPCHPDAGP - Question 3 - Select One
A, B and C are three points on a circle with centre O. The tangent at C meets BA produced to T. If ∠ATC=30∘ and ∠ACT=48∘, then what is the value of ∠AOB?
A78∘B96∘C102∘D108∘
In the given figure,two straight line AB and CD intersect at a point O.
If ∠AOC=42∘,Find the measure of each of the angles:
∠AOD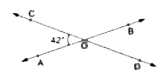
If ∠AOC=42∘,Find the measure of each of the angles:
∠BOD
If ∠AOC=42∘,Find the measure of each of the angles:
an≤COB View Solution
View SolutionFind the coordinates of the point which divides the line segment joining the points (5,−2)and(9,6) internally and externally in the ration 3 : 1
View SolutionTwo lines AB and CD intersect at a point O.∠AOC=40∘,find the measure of each of the angles ∠AOD,∠BODand∠BOC.
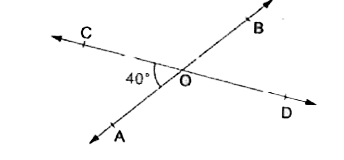 View Solution
View Solution'O' is the centre of the circle, line segment BOD is the angle bisector of ∠AOC,∠COD=50∘. Find ∠ABC :
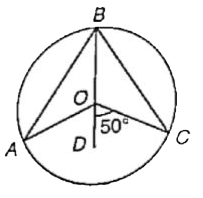 View Solution
View SolutionA cell is connected between the points A and Cofa circular conductor ABCDA of centre O. ∠AOC=60∘. If B1, and B2, are the magnitudes of the magnetic fields at O due to currents in ABC and ADC respectively, the ratio B1/B2, is
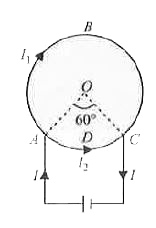 View Solution
View Solution
