Two long parallel conductors carry currents i1=3A and i2=3A both are directed into the plane of paper. The magnitude of resultant magnetic field at point 'P', is

(1) The net magnetic field →B at point P is the vector sum of the magnetic fields due to the currents in the two wires.
(2) We can find the magnetic field due to any current by applying the Biot-Savart law to the current. For points near the current in a long straight wire, that law leads to Eq.29-4.
Finding the vectors : In Fig. 29-15a, point P is distance R from both currents i1 and i2. Thus, Eq. 29-4 tells us that at point P those currents produce magnetic fields →B1 and →B2 with magnitudes
B1=μ0i12πR and B2=μ0i22πR
In the right triangle of Fig. 29-15a, note tht the base angles (between sides R and d) are both 45∘. This allows us to write cos45∘=R/d and replace R with dcos45∘. Then the field magnitudes B1 and B2 become
B1=μ0i12πdcos45∘ and B2=μ0i22πdcos45∘
We want to combine →B1 and →B2 to find their vector sum, which is the net field →B at P. To find the directions of →B1 and →B2, we apply the right-hand rule of Fig. 29-5 to each current in Fig. 29-15a. For wire 1, with current out of the page , we mentally grasp the wire with the right hand, with the thumb pointing out of the page. Then the curled fingers indicate that the field lines run counterlockwise. In, they are directed upward to the left. Recall that the magnetic field at a point near a long, straight current -carrying wire must be directed perpendicular to a radial line between the point

and the current . Thus →B1 must be directed upward to the left as drawn in Fig. 29-15b. (Note carefully the perpendicular symbol between vector B1 and the line connecting point P and wire 1)
Repeating this analysis for the current in wire 2 we find that →B2 is directed upward to the right as drawn in Fig. 29-15b.
Adding the vectors : We can now vectorially add →B1 to find the net magnetic field →B at point P, either by using a vector -capable calculator or by resolving the vectors into components and then combining the components of →B. However in Fig. 29-15b, there is a third method : Becuase →B1 and →B2 are perpendicular to each other, they form the legs of a right triangle, with →B as the hypotenuse. So,
B=√R21+R22=μ02πd(cos45∘)√i21+i22
=(4π×10−7T⋅m/A)√(15A)2+(32A)2(2π)(5.3×10−2m)(cos45∘)
−1.89×10−4T≈190μT.
The angle ϕ between the directions of →B and →B2 in Fig. 29-15b follows from
ϕ=tan−1.B1B2
which, with B1 and B2 as given above, yields
ϕ=tan−1.i1i2=tan−1.15A32A=25∘
The angle between →B and the x axis shown in Fig. 29-15b is then
ϕ+45∘=25∘+45∘=70∘
Topper's Solved these Questions
- MAGNETIC FIELDS DUE TO CURRENTSBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Check point
4 Videos
- MAGNETIC FIELDS DUE TO CURRENTSBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Problems
45 Videos
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (Integer Type)
6 Videos
- MAGNETIC FORCEBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Practice Questions (Integer type )
7 Videos
Similar Questions
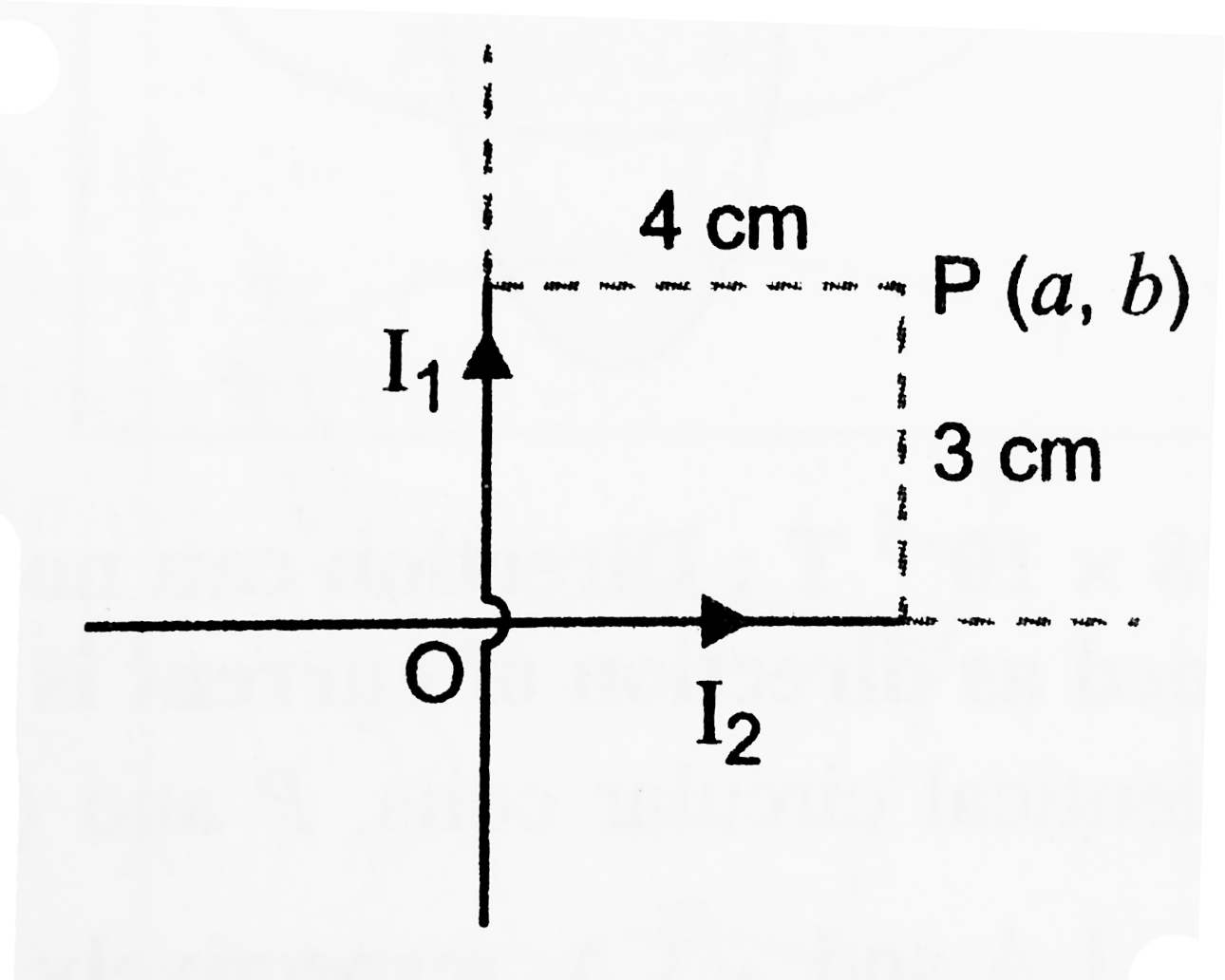
Two insulating infinite long conductors carrying currents I1(=2A) and I2(=4A) lie mutually perpendicular to each other in the same plane, as shown in figure. Find the magnetic field at the point P(a,b), where a=4cm, , b=3cm.
View SolutionTwo long parallel wires carry currents i1 and i2 such that i1>i2. When the currents are in the same direction, the magnetic field at a point midway between the wires is 6×10−6T. If the direction of i2 is reversed, the field becomes 3×10−5T. The ratio i1i2 is
View Solution
Knowledge Check
Two long parallel conductors carry currents i1=3A and i2=3A both are directed into the plaane of paper. The magnitude of resultant magnetic field at point 'P', is
 A12μTB5μTC13μTD7μT
A12μTB5μTC13μTD7μTTwo infinitely long parallel wires carry currents of magnitudeI1 and I2 and are at a distance 4 cm apart. The magnitude of the net magnetic field is found to reach a non-zero minimum values between the two wires and 1 cm away from the first wire. The ratio of the two currents and their mutual direction is
AI2I1=9, antiparallelBI2I1=9, parallelCI2I1=3, antiparallelDI2I1=3, parallelTwo long parallel straight conductors carry current i1 and i2(i1>i2). When the currents are in the same directions, the magnetic field at a point midway between the wires is 20μT. If the direction of i2 is reversed, the field becomes 50μT. The ratio of the current i1/i2 is :
A5/2B7/3C4/3D5/3
Two long parallel wires carry currents i1 and i2 such that i1>i2. When the currents are in the same direction, the magnetic field at a point midway between the wires is 6×10−6T. If the direction of i2 is reversed, the field becomes 3×10−5T. The ratio i1i2 is
View SolutionTwo long parallel straight conductors carry currents 7, and 12 (I1>I2) When the currents are in the same direction, the magnetic field at a point midway between the wires is 20 mt. If the direction of Iz is reversed, the field becomes 50 mt. The ratio of the currents
View SolutionEach of two long parallel wires carries a constant current i along the same direction . The wires are separated by a distance 2I. The magnitude of resultant magnetic induction in the symmetric plane of this system located between the wires at a distance R from each wire will be
View SolutionTwo parallel long wires carry currents i1 and i2 with i1>i2 .When the current are in the same direction, the magnetic field at a point midway between the wire is 20μT.If the direction of i1,is reversed.the field becomes 30μT.The ratio i1/i2 is
View SolutionTwo parallel, long wires carry currents t1andt2 with t1>t2. When the currents are in the same direction, the magnetic field at a point midway between the wires is 10 μT. If the direction of i2 is reversed, the field becomes 30 μT. Find the ratio i1i2.
View Solution
