A train travels due south at 30 m/s (relative to the ground) in a rain that is blown toward the south by the wind. The path of each raindrop makes an angle of 70 with the vertical, as measured by an observer stationary on the ground. An observer on the train, however, sees the drops fall perfectly vertically. Determine the speed of the raindrops relative to the ground.
To solve the problem, we need to analyze the motion of the raindrops as seen by both the observer on the ground and the observer on the train.
1. Define the Variables:
- Let the speed of the train relative to the ground be Vt=30m/s (southward).
- Let the speed of the raindrops relative to the ground be Vr.
- The angle made by the raindrops with the vertical as observed from the ground is θ=70∘.
2. Understanding the Motion:
- From the perspective of the observer on the ground, the raindrops are falling at an angle of 70∘ from the vertical. This means that the horizontal component of the velocity of the raindrops (southward) can be calculated using trigonometric functions.
3. Calculate the Horizontal Component of the Rain's Velocity:
- The horizontal component of the velocity of the rain can be expressed as:
Vr,x=Vrsin(70∘)
- Since the observer on the train sees the raindrops falling vertically, the horizontal component of the rain's velocity must equal the speed of the train:
Vr,x=Vt=30m/s
4. Set Up the Equation:
- Therefore, we have:
Vrsin(70∘)=30
5. Calculate the Speed of the Raindrops:
- Rearranging the equation gives:
Vr=30sin(70∘)
- Now, calculate sin(70∘):
sin(70∘)≈0.9397
- Substituting this value back into the equation:
Vr=300.9397≈31.9m/s
6. Final Result:
- Rounding to two significant figures, the speed of the raindrops relative to the ground is approximately:
Vr≈32m/s
- Let the speed of the train relative to the ground be Vt=30m/s (southward).
- Let the speed of the raindrops relative to the ground be Vr.
- The angle made by the raindrops with the vertical as observed from the ground is θ=70∘.
- From the perspective of the observer on the ground, the raindrops are falling at an angle of 70∘ from the vertical. This means that the horizontal component of the velocity of the raindrops (southward) can be calculated using trigonometric functions.
- The horizontal component of the velocity of the rain can be expressed as:
Vr,x=Vrsin(70∘)
- Since the observer on the train sees the raindrops falling vertically, the horizontal component of the rain's velocity must equal the speed of the train:
Vr,x=Vt=30m/s
- Therefore, we have:
Vrsin(70∘)=30
- Rearranging the equation gives:
Vr=30sin(70∘)
- Now, calculate sin(70∘):
sin(70∘)≈0.9397
- Substituting this value back into the equation:
Vr=300.9397≈31.9m/s
- Rounding to two significant figures, the speed of the raindrops relative to the ground is approximately:
Vr≈32m/s
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - CHECKPOINT3videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PROBLEMS50videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )3videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions57videos
OSCILLATIONS
Similar Questions
The figure shows a circular path taken by a particle. If the instantaneous velocity of the particle is →v=(2m/s)ˆi−(2m/s)ˆj, through which quadrant is the particle moving at that instant if it is traveling (a) clockwise and (b) counterclockwise around the circle? For both cases, draw →v on the figure.
 06:46View Solution
06:46View SolutionThe position vector for an electron is →r=(6.0m)ˆi−(4.0m)ˆj+(3.0m)ˆk. (a) Find the magnitude of →r.
View SolutionA particle is dropped from a height h and at the same instant another particle is projected vertically up from the ground. They meet when the upper one has descended a height h/3. Find the ratio of their velocities at this instant.
07:22View SolutionWhich one of the following statement is true concerning an object executing simple harmonic motion?
04:44View SolutionA man running on a horizontal road at 6 km//h finds the rain falling vertically. He doubles his speed and find that the raindrops make an angle 37^(@) with the vertical. Find the velocity of rain with respect to the ground.
02:01View SolutionRain falling vertically is appeared to fall at 37∘ with vertical for a man running on horizontal ground with 8 m/s. What is the speed of rain ( in m/s) relative to ground.
06:39View SolutionBy the term velocity of rain, we mean velocity with which raindrops fall relative to the ground. In absence of wind, raindrops fall vertically and in presence of wind raindrops fall obliqucly. Moreover raindrops acquire a constant terminal velocity due air resistance very quickly as they fall toward the carth. A moving man relative to himself observes an altered velocity of raindrops. Which is known as velocity of rain relative to the man. It is given by the following equation.
→vrm=→vr−→vm
A standstill man relative to himself observes rain falling with velocity, which is equal to velocity of the raindrops relative to the ground. To protect himself a man should his umbrella against velocity of raindrops relative to himself as shown in the following figure.

Rain is falling vertically with velocity 80 cm/s.
(a) How should you hold your umbrella ?
(b) You start walking towards the east with velocity 60 cm/s. How should you hold umbrella ?
(c) You are walking towards the west with velocity 60 cm/s. How should you hold your umbrella ?
(d) You are walking towards the north with velocity 60 cm/s. How should you hold your umbrella?
(e) You are walking towards the south with velocity 80 cm/s. How should you hold your umbrella ?11:52View SolutionBy the term velocity of rain, we mean velocity with which raindrops fall relative to the ground. In absence of wind, raindrops fall vertically and in presence of wind raindrops fall obliqucly. Moreover raindrops acquire a constant terminal velocity due air resistance very quickly as they fall toward the carth. A moving man relative to himself observes an altered velocity of raindrops. Which is known as velocity of rain relative to the man. It is given by the following equation.
→vrm=→vr−→vm
A standstill man relative to himself observes rain falling with velocity, which is equal to velocity of the raindrops relative to the ground. To protect himself a man should his umbrella against velocity of raindrops relative to himself as shown in the following figure.

When you are standstill in rain, you have to hold umbrella vertically to protect yourself.
(a) When you walk with velocity 90 cm/s, you have to hold your umbrella at 53∘ above the horizontal. What is velocity of the raindrops relative to the ground and relative to you ?
(b) If you walk with speed 160 cm/s, how should you hold your umbrella ?03:36View SolutionBy the term velocity of rain, we mean velocity with which raindrops fall relative to the ground. In absence of wind, raindrops fall vertically and in presence of wind raindrops fall obliqucly. Moreover raindrops acquire a constant terminal velocity due air resistance very quickly as they fall toward the carth. A moving man relative to himself observes an altered velocity of raindrops. Which is known as velocity of rain relative to the man. It is given by the following equation.
→vrm=→vr−→vm
A standstill man relative to himself observes rain falling with velocity, which is equal to velocity of the raindrops relative to the ground. To protect himself a man should his umbrella against velocity of raindrops relative to himself as shown in the following figure.
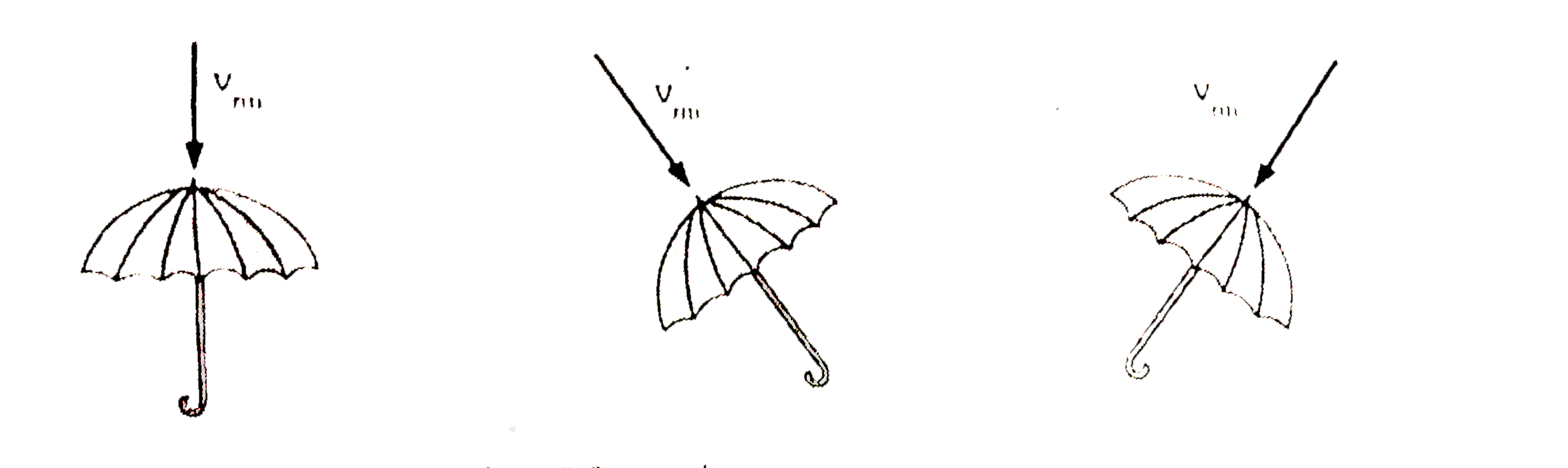
A man walks in rain at 72 cm/m due east and observes the rain falling vertically. When he stops, rain appears to strike his back at 37∘ from the vertical. Find velocity of raindrops relative to the ground.View SolutionBy the term velocity of rain, we mean velocity with which raindrops fall relative to the ground. In absence of wind, raindrops fall vertically and in presence of wind raindrops fall obliqucly. Moreover raindrops acquire a constant terminal velocity due air resistance very quickly as they fall toward the carth. A moving man relative to himself observes an altered velocity of raindrops. Which is known as velocity of rain relative to the man. It is given by the following equation. vec(v)_(rm)=vec(v)_(r)-vec(v)_(m) A standstill man relative to himself observes rain falling with velocity, which is equal to velocity of the raindrops relative to the ground. To protect himself a man should his umbrella against velocity of raindrops relative to himself as shown in the following figure. When you walk in rain at 75 cm/s, you have to hold your umbrella vertically and when you double your speed in the same direction, you have to hold your unbrella at 53^(@) above the horizontal. what is the rain velocity ?
03:06View SolutionAt a particular instant, a stationary observer on the ground sees a package falling with a speed v1 at an angle θ to the vertical. To a pilot flying horizontally with a constant speed v relative to the ground, the package appears to be falling verically with a speed v2 (at that same instant).
The speed of the pilot relative to the ground (v) is02:58View SolutionDuring a rainstorm the raindrops are observed to strike the ground at an angle of 37∘ with the vertical. The wind speed is 4.5 m/s. Assuming that the horizontal velocity component of the raindrops is same as the speed of air, what is the vertical component of raindrops? What is their speed ?
04:39View SolutionA southward wind of speed 5 m/s affects raindrops falling vertically at 4 m/s. A cyclist moves towards south with a speed of 2m/s . What are the magnitude and direction of the speed of the raindrops relative to the cyclist ?
06:53View SolutionA passanger sitting in a train moving with constant horizontal velocity drops a ball vertically downward what is the path observed by a man standing on the ground near the train and
06:50View SolutionDuring a rainstorm the raindrops are observed to strike the ground at an angle of 37∘ with the vertical. The wind speed is 4.5 m/s. Assuming that the horizontal velocity component of the raindrops is same as the speed of air, what is the vertical component of raindrops? What is their speed ?
03:54View Solution
