A particle thrown up vertically reaches its highest point in time t1 and returns to the ground in a further time t2. The air resistance exerts a constant force on the particle opposite to its direction of motion.
t1=t2
t1>t2
t1<t2
Information is not sufficient to decide the relation between t1 and t2
The correct Answer is:c
When the particle moves upwards then its weight as the well as the air resistance both acts downwards hence the retardation for the upward journey can be calculated as follows:
Mg+F=Ma1
⇒a1=g+FM
When particle moves downward then weight acts downwards but air resistance acts upwards, hence the acceleration during the downward journey can be calculated as follows:
Mg−F−Ma2
⇒a2=g−FM
If h is the maximum height attained by the particle then we can write the following:
h=12a1t21=12a2t22
t2t1=(√a1a2)
From equation 1 and 2 we can see that a1>a2 hence t2>t1
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:COMPETITION FILE ( B.(MULTIPLE CHOICE QUESTIONS))
Explore 74 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:COMPETITION FILE ( C.(MULTIPLE CHOICE QUESTIONS))
Explore 13 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:REVISION EXERCISE (NUMERICAL PROBLEMS )
Explore 7 Videos
- MOTION IN A PLANE Book:MODERN PUBLICATIONChapter:MOTION IN A PLANE Exercise:Chapter Practice Test
Explore 15 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Practice Test (For Board Examination)
Explore 12 Videos
Similar Questions
Knowledge Check
A particle thrown up vertically reaches its highest point in time t1 and returns to the ground in a further time t2. The air resistance exerts a constant force on the particle opposite to its direction of motion.
At1>t2Bt1=t2Ct1<t2Dmay be (A) or (C) depending on the ratio of the force of air resistance to the wight of the particle.A particle is thrown vertically upwards with a velocity v. It returns to the ground in time T. which of the following graphs correctly represents the motion ?
A B
B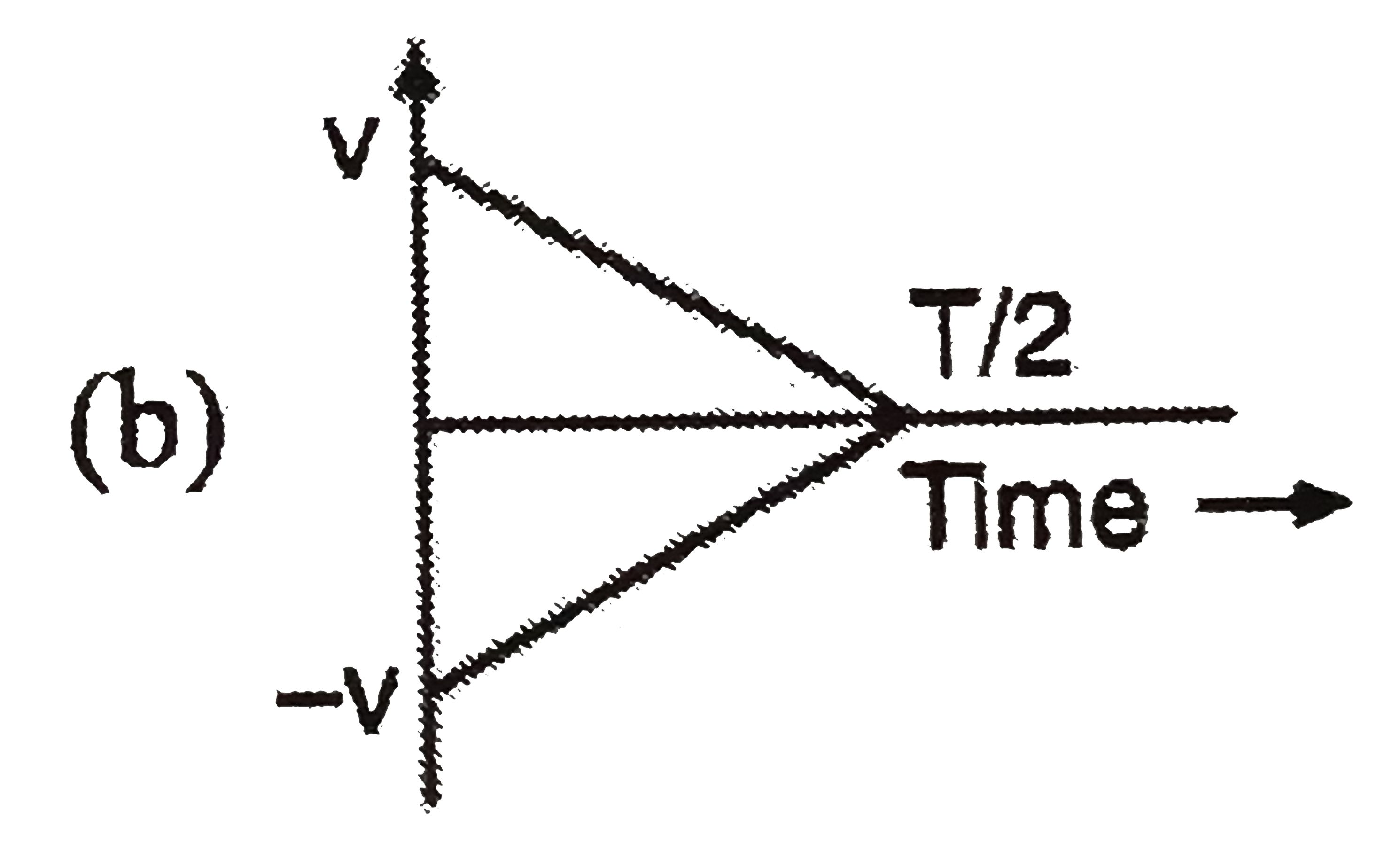 C
C D
D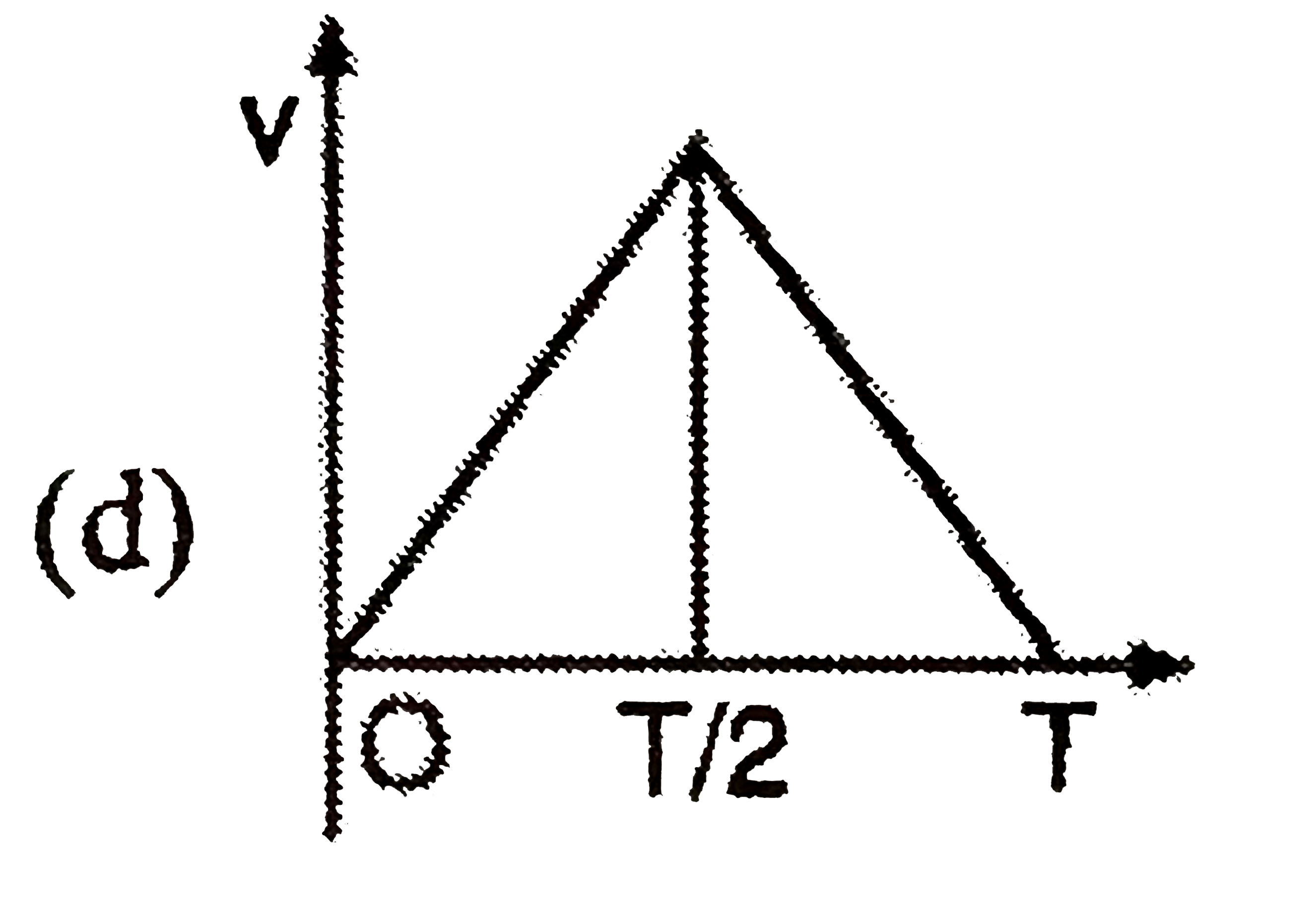
From the top of a tower a stone is thrown up which reaches the ground in time t1. A second stone thrown down with the same speed reaches the ground in a time t2. A third stone released from rest from the same location reaches the ground in a time t3. then:
A1t3=1t1+1t2Bt23=t21−t22Ct3=t1+t22Dt3=√t1t2
A particle thrown up vertically from the ground at reaches its highest point at t=t0 =The displacement of the particle between t=7t08andt=t0 is S. Then u2Sg=
View SolutionA particle is projected vertically upwards and reaches the maximum height H in time T. The height of the partlcle at any time t(<T) will be
View SolutionA ball is thrown vertically upwards from the ground. If T1 and T2 are the respective time taken in going up and coming down, and the air resistance is not ignored, then
View SolutionFrom the top of a tower, a stone is thrown up and reaches the ground in time t1=9s. a second stone is thrown down with the same speed and reaches the ground in time t2=4s. A third stone is released from rest and reaches the ground in time t3, which is equal to
View SolutionA particle is projected vertically upwards and it reaches the maximum height H in time T seconds. The height of the particle at any time t will be-
View Solution

