A uniform ball, of mass M = 6.00 kg and radius R, rolls smoothly from rest down a ramp at angle θ=30.0∘ .
What are the magnitude and direction of the frictional force on the ball as it rolls down the ramp?
To solve the problem of finding the magnitude and direction of the frictional force acting on a uniform ball rolling down a ramp, we can follow these steps:
Step 1: Identify the Forces Acting on the Ball
When the ball rolls down the ramp, the forces acting on it include:
- The gravitational force (weight) acting downward, W=Mg.
- The normal force N acting perpendicular to the ramp.
- The frictional force f acting up the ramp (opposing the motion).
Step 2: Resolve the Gravitational Force
The gravitational force can be resolved into two components:
- Perpendicular to the ramp: W⊥=Mgcos(θ)
- Parallel to the ramp: W∥=Mgsin(θ)
Given M=6.00kg and θ=30∘:
- W∥=6.00⋅g⋅sin(30∘)=6.00⋅g⋅0.5=3.00g
- W⊥=6.00⋅g⋅cos(30∘)=6.00⋅g⋅√32=3√3g
Step 3: Apply Newton's Second Law
For the ball rolling down the ramp, we can apply Newton's second law in the direction parallel to the ramp:
Mgsin(θ)−f=Ma
Where a is the linear acceleration of the center of mass of the ball.
Step 4: Relate Linear Acceleration to Angular Acceleration
For a rolling ball, the linear acceleration a is related to the angular acceleration α by:
a=Rα
The moment of inertia I for a solid sphere is given by:
I=25MR2
Using the relationship between torque and angular acceleration, we have:
fR=Iα=25MR2α
Substituting α=aR:
fR=25MR2⋅aR⟹f=25Ma
Step 5: Substitute for a
From the equation of motion:
Mgsin(θ)−f=Ma⟹3g−f=Ma
Substituting f=25Ma:
3g−25Ma=Ma⟹3g=Ma+25Ma=75Ma
Solving for a:
a=15g7M
Step 6: Calculate the Frictional Force
Now substituting back to find f:
f=25Ma=25M⋅15g7M=6g7
Substituting g≈9.81m/s2:
f=6⋅9.817≈8.4N
Step 7: Determine the Direction of the Frictional Force
The direction of the frictional force is up the ramp, opposing the motion of the ball as it rolls down.
Final Answer
The magnitude of the frictional force is approximately 8.4N and it acts up the ramp.
---
When the ball rolls down the ramp, the forces acting on it include:
- The gravitational force (weight) acting downward, W=Mg.
- The normal force N acting perpendicular to the ramp.
- The frictional force f acting up the ramp (opposing the motion).
The gravitational force can be resolved into two components:
- Perpendicular to the ramp: W⊥=Mgcos(θ)
- Parallel to the ramp: W∥=Mgsin(θ)
- W∥=6.00⋅g⋅sin(30∘)=6.00⋅g⋅0.5=3.00g
- W⊥=6.00⋅g⋅cos(30∘)=6.00⋅g⋅√32=3√3g
For the ball rolling down the ramp, we can apply Newton's second law in the direction parallel to the ramp:
Mgsin(θ)−f=Ma
Where a is the linear acceleration of the center of mass of the ball.
For a rolling ball, the linear acceleration a is related to the angular acceleration α by:
a=Rα
The moment of inertia I for a solid sphere is given by:
I=25MR2
Using the relationship between torque and angular acceleration, we have:
fR=Iα=25MR2α
Substituting α=aR:
fR=25MR2⋅aR⟹f=25Ma
From the equation of motion:
Mgsin(θ)−f=Ma⟹3g−f=Ma
Substituting f=25Ma:
3g−25Ma=Ma⟹3g=Ma+25Ma=75Ma
Solving for a:
a=15g7M
Now substituting back to find f:
f=25Ma=25M⋅15g7M=6g7
Substituting g≈9.81m/s2:
f=6⋅9.817≈8.4N
The direction of the frictional force is up the ramp, opposing the motion of the ball as it rolls down.
The magnitude of the frictional force is approximately 8.4N and it acts up the ramp.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - EXAMPLE1videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - CHECKPOINT4videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE))3videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (Integer Type)4videos
TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION
Similar Questions
A uniform ball, of mass M = 6.00 kg and radius R, rolls smoothly from rest down a ramp at angle θ=30.0∘ .
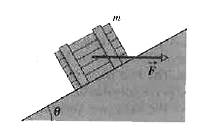
(a) The ball descends a vertical height h = 1.20 m to reach the bottom of the ramp. What is its speed at the bottom?View SolutionIn Fig. 5-45, a crate of mass m = 115 kg is pushed at constant speed up a frictionless ramp (θ=30.0∘) by a horizontal force →F. What are the magnitudes of (a) →F and (b) the force on the crate from the ramp ?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A solid cylinder of mass M and radius R rolls from rest down a plane inclined at an angle θ to the horizontal. The velocity of the centre of mass of the cylinder after it has rolled down a distance d is :
A√23gdtanθB√gdtanθC√34gdsinθD√43gdsinθ - Question 2 - Select One
A uniform sphere of mass m and radius r rolls without slipping down a inclined plane, inclined at an angle 45∘ to the horizontal . Find the magnitude of frictional coefficient at which slipping is absent :
A13B27C15D17

A ball of mass m and radius r rolls along a circular path of radius R its speed at the bottom (θ=0∘) of the path is v0 find the force of the path on the ball as a function of θ.View Solution(a) A rigid body of radius of gyration k and radius R rolls without slipping down a plane inclined at an angle θ with the horizontal. Calculate its acceleration and the frictional force acting on it.
(b) If the body be in the form of a disc and θ=30∘, what will be the acceleration and the frictional force acting on it.View SolutionA solid cylinder of mass 8 kg and radius 50 cm is rolling down a plane inclined at an angle of 30∘ with the horizontal. The minimum value of coefficient of friction so that cylinder does not slip while rolling down the plane.
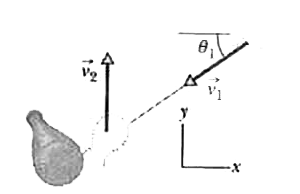
View SolutionFigure shows a 0.300 kg baseball just before and just after it collides with a bat. Just before, the ball has velocity →v1 of magnitude 12.0 m/s and angle θ1=35.0∘ Just after, it is traveling directly upward with velocity →v2 of magnitude 10.0 m/s The duration of the collision is 2.00 ms. What are the (a) magnitude and (b) direction (relative to the positive direction of the x axis) of the impulse on the ball from the bat? What are the (c) magnitude and (d) direction of the average force on the ball from the bat?
 View Solution
View SolutionA uniform hoop, disk, and sphere, with the same mass M and same radius R, are released simultaneously from rest at the top of a ramp of length L = 2.5 m and angle θ=12∘ with the horizontal. The objects roll smoothly down the ramp.
What is vcom for each object at the bottom of the ramp?View SolutionA uniform hoop, disk, and sphere, with the same mass M and same radius R, are released simultaneously from rest at the top of a ramp of length L = 2.5 m and angle θ=12∘ with the horizontal. The objects roll smoothly down the ramp.
(a) Which object wins the race to the bottom of the ramp?View Solution
