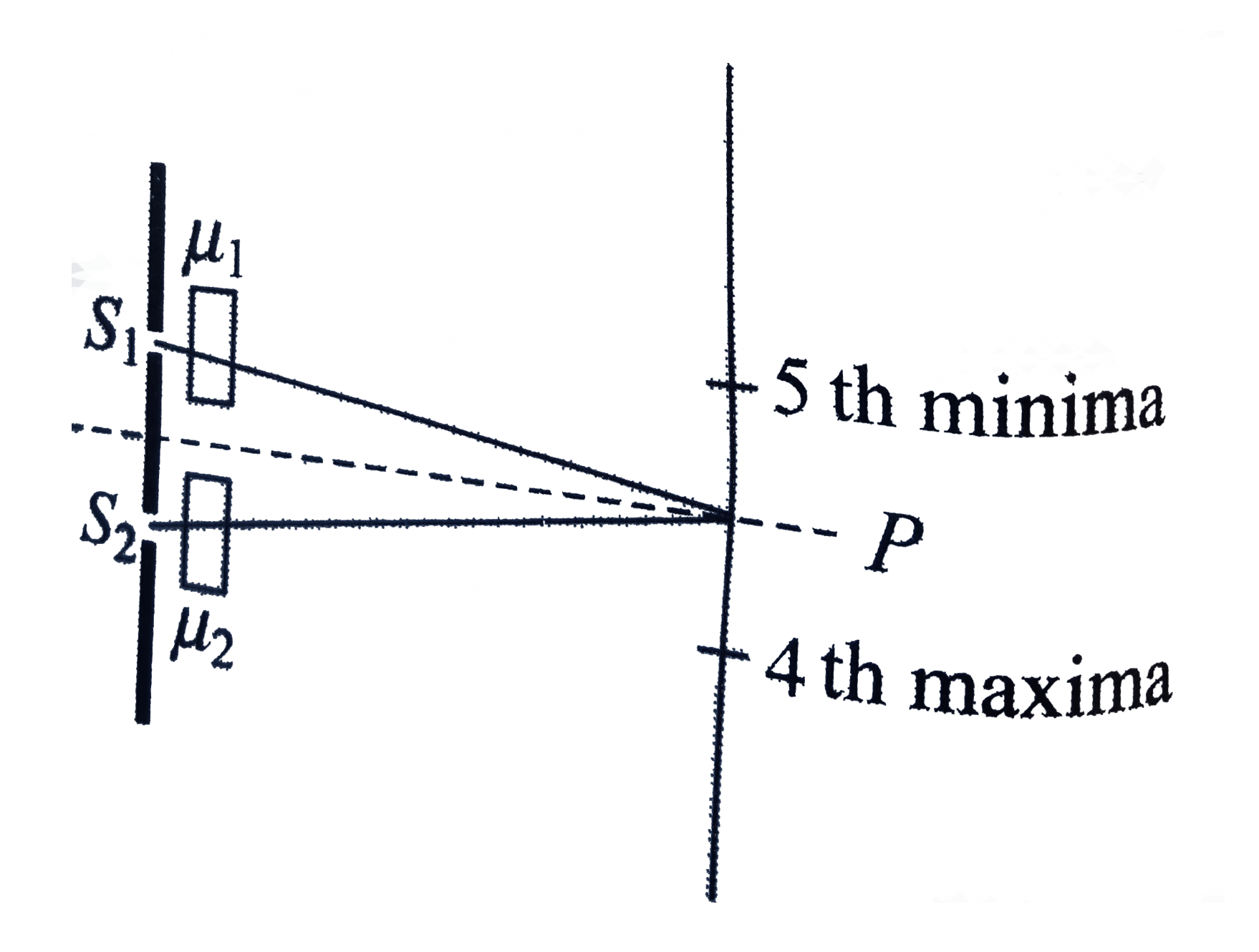
In Young's experiment the upper slit is covered by a thin glass plate of refractive index 1.4 while the lower slit is covered by another glass plate, having the same thickness as the first one but having refractive index 1.7 interference pattern is observed using light of wavelength 5400Å
It is found that point P on the screen where the central maximum (n=0) fell before the glass plates were inserted now has 3/4 the original intensity. It is further observed that what used to be the fourth maximum earlier, lies below point P while the fifth minimum lies above P.
Calculate the thickness of glass plate. (Absorption of light by glass plate may be neglected.
 .
.
KEY IDEA
In Young.s double-slit experiment, slits S1 and S2 are equidistant from the source S and the slits have equal widths. Hence, light emerging from S1 and S2 has the same intensity, say I0. Before the plates are introduced, the path difference (and hence the phase difference ϕ) at the central point P between the interfering waves is zero.
Calculation: The intensity at point P is
I=I0+I0+2√I0I0cos0∘=4I0.
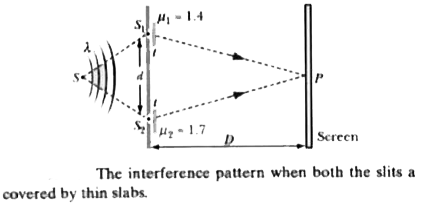
When the two plates are introduced, the path difference at the central point p between the interfering waves becomes
Δ=(μ2−1)t−(μ1−1)t=(μ2−μ1)t.
Therefore, the phase difference is given by
ϕ=2πΔλ=2πλ(μ2−μ1)t.
Hence, the intensity at point P becomes
I.=I0+I0+2√I0I0cosϕ=2I0+2I0cosϕ
It is given that
I.=3I4=34×4I0=3I0.
Thus
3I0=2I0+2I0cosϕ.
Now
cosϕ=12
ϕ=π3,5π3,7π3,11π3,13π3,......
ϕ=π3(6m±1), m= 0, 1, 2, 3,.... (35-40)
where the negative value ϕ=−π/3 corresponding to m = 0 is not admissible since ϕ is positive as μ2>μ1. The upward shift of the interference pattern due to the upper plate is
(Δy)1=(μ1−1)tDd.
The downward shift due to the lower plate is
(Δy)2=(μ2−1)tDd.
Therefore, the new downward shift is
Δy=(Δy)2−(Δy)1=(μ2−μ1)tDd
=(1.7−1.4)tDd=0.3tDd
Now, the distance of the fifth maximum from P is 5λD/d, and the distance of sixth minimum from P is [6−(1/2)]λD/d=5.5λD/d. It is given that the net shift lies between 5λD/d and 5.5λD/d, that is
5λDd<0.3tDd<5.5λDd
5λ0.3<t<5.5λ0.3
5×5.4×10−70.3m<t<5.5×5.4×10−70.3m
9.0×10−6m<t<9.9×10−6m. (35−41)
We have seen that the phase difference,
ϕ=2πλ(μ2−μ1)t
=2πλ(1.7−1.4)t
=2πλ(0.3)t (35−42)
Using Eqs. 35-41 and 35-42, we have
π3(6m±1)=2πλ(0.3t)
6m±1=6λ(0.3)t=1.8t5.4×10−7
t=3(6m±1)×10−7m. (35−43)
It is clear that Eq. 35-43 will yield a value of t which satis- fies the requirement (Eq. 35-41) if m= 5. Hence,
t=3(6×5±1)×10−7
=3(30±1)×10−7
=9.3×10−6m or 8.7×10−6m.
The value of t=8.7×10−6m does not satisfy the require- ment in Eq. 35-40. Hence, t=9.3×10−6m.
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - CHECKPOINT
6 Videos
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PROBLEMS
61 Videos
- HYDROGEN ATOMBOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PRACTICE QUESTIONS(Integer Type)
6 Videos
- MAGNETIC FIELDS DUE TO CURRENTSBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Integer Type)
4 Videos
Similar Questions
The figure shows a monochromatic ray of light traveling across parallel interfaces, from an original material a, through layers of materials b and c, and then back into material a. Rank the materials according to the speed of light in them, greatest first.

View Solution
In Figure, a broad bcam Incident light of light of wavelength 630 nn is sent directly downward through the top plate of a pair of glass plates touching at the left end. The air between the plates acts as a thin film, and an interference pattern can be seen from above the plates. Initially, a dark fringe lies at the left end, a bright fringe lies at the right end, and nine dark fringes lie between those two end fringes. The plates are then very gradually squeezed together at a constant rate to decrease the angle between them. As a result, the fringe at the right side changes between being bright to being dark every 15.0 s. (a) At what rate is the spacing between the plates at the right end being changed? (b) By how inuch has the spacing there changed when both left and right ends have a dark fringe and there are five dark fringes between them?
View SolutionThe radius of hydrogen atom in its ground state is 5.3×10−11m. After collision with an electron, it is found to have a radius of 21.2×10−11m. What is the principal quantum number of the final state of the atom?
View SolutionA steady current I goes through a wire loop PQR having shape of a right angle triangle with PQ=3x,PR=4xandQR=5x. If the magnitude of the magnetic field at P due to this loop is k(μ0I48πx), find the value of K.
View SolutionIn Young's experiment the upper slit is covered by a thin glass plate of refractive index 1.4 while the lower slit is covered by another glass plate, having the same thickness as the first one but having refractive index 1.7 interference pattern is observed using light of wavelength 5400 Å It is found that point P on the screen where the central maximum (n = 0) fell before the glass plates were inserted now has 3//4 the original intensity. It is further observed that what used to be the fourth maximum earlier, lies below point P while the fifth minimum lies above P. Calculate the thickness of glass plate. (Absorption of light by glass plate may be neglected. .
View SolutionA light of wavelength 6000 Å shines on two narrow slits separeted by a distance 1.0 mm and illuminates a screen at a distance 1.5 m away. When one slit is covered by a thin glass plate of refractive index 1.8 and other slit by a thin glass plate of refractive index mu , the central maxima shifts by 0.1 rad. Both plates have the same thickness of 0.5 mm. The value of refractive index mu of the glass is
View SolutionOne slit of a double slits experiment is covered by a thin glass plate of refractive index 1.4 and the other by a thin glass plate of refractive index 1.7 .The point on the screen ,where central bright fringe was formed before the introduction of the glass sheets,is now occupied by the 15th bright fringe.Assuming that both the glass plates have same thickness and wavelength of light used in 4800Å ,find the their thickness.
View SolutionA thin glass plate of thickness t and refractive index mu is between screen &one of the slits in young's experiment.if the intensity at the center of the screen is I ,was the intenstity at the same point prior to the introduction of the sheet. (b) One slit of a young's experiment is covered by a glass plate (mu_(1)=1.4) and the other by another glass plate (mu_(2)=1.7) of the same thickness. The point of central maxima of the screen,before the plates were introduced is now occupied by the third bright fringe.Find the thicknes of the thickness of the plates.the wavelength of light used in 4000Å .
View SolutionIn young's experiment, the upper slit is covered by a thin glass plate of refractive index 43 and of thickness 9λ, where λ is the wavelength of light used in the experiment. The lower slit is also covered by another glass plate of thickness 2D & refractive index 32, as shown in figure. If I0 is the intensity at point P due to slits S1 & S2 each, then:

View SolutionIn Young’s double slit experiment, the upper slit is covered by a thin glass plate of refractive index 1.4 while the lower slit is covered by another glass plate having same thickness as the first one but having refractive index 1.7.
Interference pattern is observed using light of wavelength5400∘A. It is found that the point P on the screen where the central maximum fell before the glass plates were inserted, now has 34 the original intensity. It is also observed that what used to be 5th maximum earlier, lies below the point P while the6th minimum lies above P. Calculate the thick- ness of glass plates. Absorption of light by glass plate may be neglected.
View SolutionIn a Young's experimenttje upper slit is covered by a thin glass plate of refractive index. 1.4 while the lower slit is covered with another glass plate, having the same thickness as the first one but having refravtive index 1.7. Interference pattern is observed using light of wavelength 5400Å. It is found that the point P on the sreen where the central where the central maximum (n=0) fell before the glass plates were inserted now has 3/4 the original intensity. It is further observed that what used to be the fifth maximum earlie, lies shown the point P while the sixth minimum lies above P. Calculate the thickness of glass plate. (Absorption of light by a glass may be neglected).
View SolutionIn a Young's experiment, the upper slit is covered by a thin glass plate of refractive index 1.4 while the lower slit is covered by another glass plate having the same thickness as the first ont but having refractive index 1.7. Interference pattern is observed using light of wavelength 5400 A. It is found that the point P on the screen where the central maximum fell berore the glass were inserted now has (3//4)^(th) the original intensity. It is further observed that what used to be the 5th maximum earlier, Iies below the point O while the 6th minimum lies above O. The thickness of the glass plate in nxx10^(-7)m. Find the value of n (Absorption of light by glass plate may by neglected)
View SolutionIn Young's experiment, the upper slit is covered by a thin glass plate of refractive index 1.4 while the lower slit is covered another glass plate having the same thickness as the first one but having refractive index Interference pattern is observed using light of wavelength 5400A. It is observed that the point P on the screen where the central maximum (n=0) fell before the glass were inserted now has 3/4 th original intensity. It is further observed that what used to be the fifth maximum earlier, lies below the point P while the sixth minimum lies above P. Calculate the thickness of the glass plate.
View Solutionयंग के प्रयोग में, ऊपरी स्लिट को 1.4 अपवर्तनांक की काँच की पतली पट्टी से ढका गया है जबकि निचली स्लिट को एक अन्य काँच की पट्टी से जिसकी मोटाई पहली पट्टी के समान है, परन्तु अपवर्तनांक 1.7 है, से ढका गया है | 5400Å तरंगदैर्ध्य के प्रकाश से व्यतिकरण प्रतिरूप प्राप्त किया जाता है | यह पाया जाता है कि पर्दे के बिंदु P पर जहाँ काँच की पट्टियाँ लगाने से पहले केंद्रीय उच्चिष्ठ तीव्रता (n=0) थी | वहाँ पर अब तीव्रता पहले की 3/4 है | यह भी देखा जाता है, कि पहले की पाँचवीं अधिकतम तीव्रता अब बिंदु P के नीचे है जबकि छठी न्यूनतम तीव्रता P के ऊपर है | काँच की पट्टियों की मोटाई ज्ञात कीजिए ( काँच की पत्तियों द्वारा प्रकाश का अवशोषण छोड़ा जा सकता है ) |
View SolutionIn Young’s experiment, the upper slit is covered by a thin glass plate of refractive index 1.4, while the lower slit is covered by another glass plate having the same thickness as the first one but having the refractive index 1.7. Interference pattern is observed using light of wavelength 5400 Å . It is found that the point P on the screen where central maximum (n = 0) fall before the glass plate were inserted, now has % the original intensity. It is further observed that what used to be the fifth maximum earlier lies below the point P while the sixth minima lies above P. Calculate the thickness of glass plate. (Absorption of light by glass plate may be neglected).
View Solutionद्विस्लिट प्रयोग में 4800Å तरंगदैर्ध्य वाला प्रकाश प्रयुक्त करते हुए फ्रिंज उत्पन्न होते है। एक स्लिट, काँच (μ=1.4) की पतली प्लेट से ढंकी जाती है और दूसरी स्लिट उतनी ही मोटी काँच (परन्तु μ=1.7) की प्लेट से ढंकी जाती है । ऐसा करने पर केंद्रीय फ्रिंज उस स्थिति की ओर विस्थापित हो जाता है जहाँ पहले केंद्र से पांचवा दीप्त फ्रिंज था। प्लेट की मोटाई निकाले।
View Solution
