A uniform magnetic field passes through two areas, and . The angles between the magnetic field and the normals of areas and are 30.0° and 60.0°, respectively. If the magnetic flux through the two areas is the same, what is the ratio ?
0.577
1
0.816
1.23
The correct Answer is:A
To solve the problem of finding the ratio A1A2 given that the magnetic flux through the two areas A1 and A2 is the same, we can follow these steps:
Step 1: Understand the Magnetic Flux Formula
The magnetic flux Φ through an area A in a magnetic field B is given by the formula:
Φ=B⋅A⋅cos(θ)
where θ is the angle between the magnetic field and the normal (perpendicular) to the area.
Step 2: Write the Flux Equations for Both Areas
For area A1 with angle θ1=30∘:
Φ1=B⋅A1⋅cos(30∘)
For area A2 with angle θ2=60∘:
Φ2=B⋅A2⋅cos(60∘)
Step 3: Set the Fluxes Equal
Since the problem states that the magnetic flux through both areas is the same, we can set Φ1 equal to Φ2:
B⋅A1⋅cos(30∘)=B⋅A2⋅cos(60∘)
Step 4: Cancel Out Common Terms
We can cancel B from both sides of the equation (assuming B is not zero):
A1⋅cos(30∘)=A2⋅cos(60∘)
Step 5: Solve for the Ratio A1A2
Rearranging the equation gives:
A1A2=cos(60∘)cos(30∘)
Step 6: Substitute the Values of Cosines
Using known values:
cos(30∘)=√32andcos(60∘)=12
Substituting these values into the ratio:
A1A2=12√32=1√3
Step 7: Final Result
Thus, the ratio A1A2 is:
A1A2=1√3≈0.577
The magnetic flux Φ through an area A in a magnetic field B is given by the formula:
Φ=B⋅A⋅cos(θ)
where θ is the angle between the magnetic field and the normal (perpendicular) to the area.
For area A1 with angle θ1=30∘:
Φ1=B⋅A1⋅cos(30∘)
For area A2 with angle θ2=60∘:
Φ2=B⋅A2⋅cos(60∘)
Since the problem states that the magnetic flux through both areas is the same, we can set Φ1 equal to Φ2:
B⋅A1⋅cos(30∘)=B⋅A2⋅cos(60∘)
We can cancel B from both sides of the equation (assuming B is not zero):
A1⋅cos(30∘)=A2⋅cos(60∘)
Rearranging the equation gives:
A1A2=cos(60∘)cos(30∘)
Using known values:
cos(30∘)=√32andcos(60∘)=12
Substituting these values into the ratio:
A1A2=12√32=1√3
Thus, the ratio A1A2 is:
A1A2=1√3≈0.577
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)
13 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Linked Comprehension)
19 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PROBLEMS
67 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
- ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT EXERCISE - Practice Questions (Integer)
7 Videos
Similar Questions
Knowledge Check
A regular pentagons is inscribed in a circle. If A1 and A2 represents the area of circle and that of regular pentagon respectively, then A1:A2 is
Aπ5cos(2π)5B2π5sin(2π)5C2π5 cosec 2π5D2π5cos(2π)5If A1 and A2 be areas of two regular polygons having the same perimeter and number of sides be n and 2n respectively, then : A1A2 is
A2sin(πn)1+cos(πn)B2cos(πn)1+sin(πn)C2cos(πn)1+cos(πn)D2sin(πn)1+sin(πn)The corresponding medians of two similar triangles are in the ratio 4:7. Let their respective areas be A1 and A2.A1:A2=…
A0.70069444444444B0.17152777777778C0.29444444444444D2.0527777777778
If the area of circle is A1 and area of regular pentagon inscibed in the circle is A2, then find the ratio of area of two.
View SolutionThe line that joins the saturn to the sun sweeps area A1,A2 and A3 in time intervals of 6 weeks, 3 weeks and 2 weeks respectively as shows in the Fig. What is the correct relation between A1,A2 and A3?
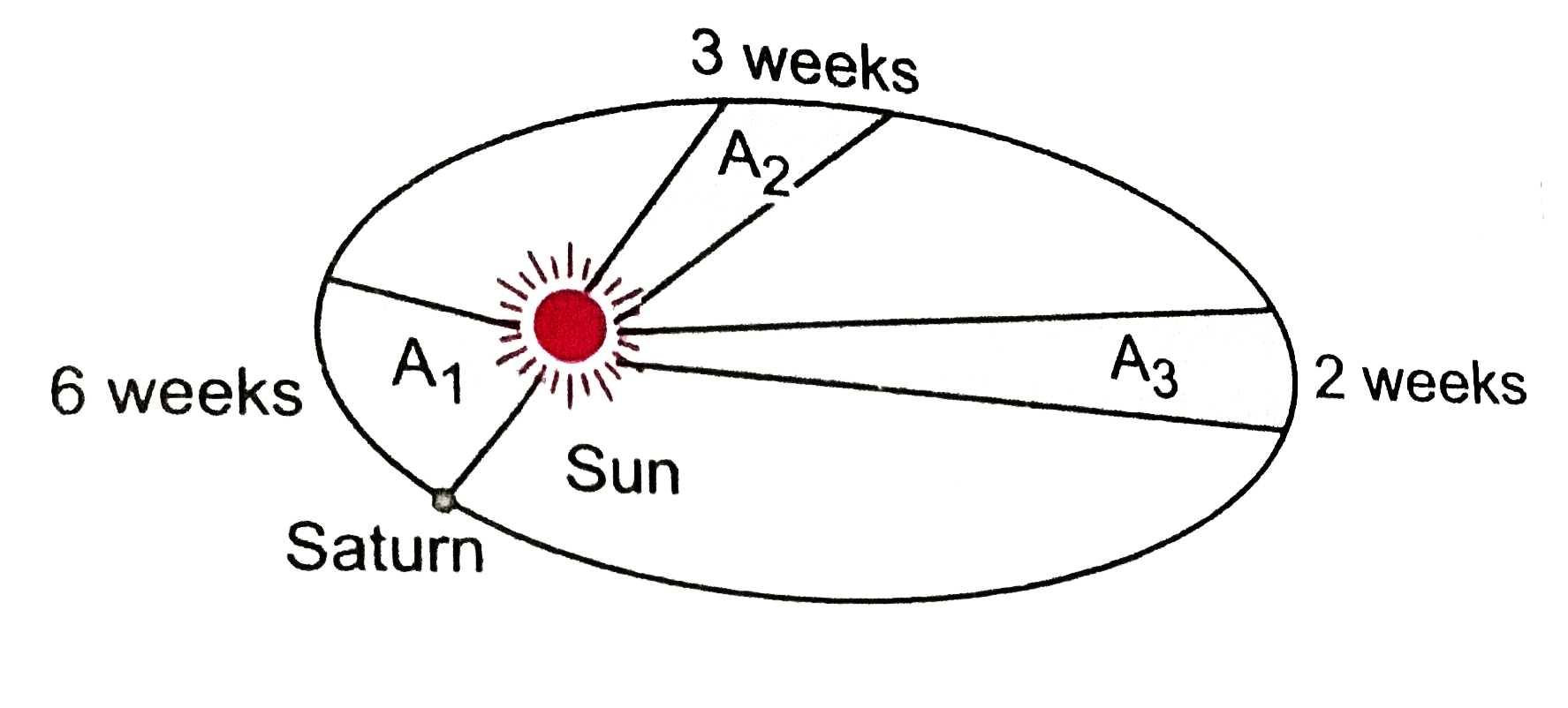
View SolutionThe line that joins the saturn to the sun sweeps area A1,A2 and A3 in time intervals of 6 weeks, 3 weeks and 2 weeks respectively as shows in the Fig. What is the correct relation between A1,A2 and A3?

View SolutionIf the area of the circle is A1 and the area of the regular pentagon inscribed in the circle is A2, then find the ratio A1A2.
View SolutionThe corresponding medians of two similar triangles are in the ratio 4:7 . Let their respective areas be A1 and A2⋅A1:A2=…… .
View Solution