If in a triangle ABC, the angles at B and Care 1.5 and 2.5 times of the angle at A respectively, then angle at B is
36∘
54∘
48∘
72∘
The correct Answer is:B
To solve the problem, we need to find the angle at B in triangle ABC, given that the angles at B and C are 1.5 and 2.5 times the angle at A, respectively.
1. Define the angles:
Let the angle at A be x.
Then, the angle at B can be expressed as 1.5x and the angle at C as 2.5x.
2. Use the triangle angle sum property:
The sum of the angles in a triangle is always 180 degrees. Therefore, we can write the equation:
x+1.5x+2.5x=180
3. Combine like terms:
Adding the coefficients of x:
(1+1.5+2.5)x=180
This simplifies to:
5x=180
4. Solve for x:
To find x, divide both sides of the equation by 5:
x=1805=36
5. Find the angle at B:
Now that we have x, we can find the angle at B:
Angle at B=1.5x=1.5×36=54
Thus, the angle at B is 54 degrees.
Summary:
- Angle A = 36 degrees
- Angle B = 54 degrees
- Angle C = 90 degrees (not needed for the answer but can be calculated)
Let the angle at A be x.
Then, the angle at B can be expressed as 1.5x and the angle at C as 2.5x.
The sum of the angles in a triangle is always 180 degrees. Therefore, we can write the equation:
x+1.5x+2.5x=180
Adding the coefficients of x:
(1+1.5+2.5)x=180
This simplifies to:
5x=180
To find x, divide both sides of the equation by 5:
x=1805=36
Now that we have x, we can find the angle at B:
Angle at B=1.5x=1.5×36=54
- Angle A = 36 degrees
- Angle B = 54 degrees
- Angle C = 90 degrees (not needed for the answer but can be calculated)
Similar Questions
Knowledge Check
In right angled ΔABC,∠B=90∘, if P and Q are points on the sides AB and BC respectively, then :
 AAQ2+CP2=2(AC2+PQ2)BAQ2+CP2=AC2+PQ2C(AQ2+CP2)=12(AC2+PQ2)D(AQ+CP)=12(AC+PQ)
AAQ2+CP2=2(AC2+PQ2)BAQ2+CP2=AC2+PQ2C(AQ2+CP2)=12(AC2+PQ2)D(AQ+CP)=12(AC+PQ)In given triangle ABC ,OB and OC are bisectors of ∠Ba nd ∠C respectively then ∠BOC is equal to
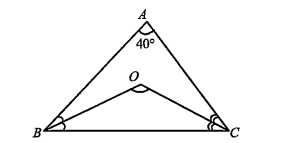 A70∘B110∘C140∘D80∘
A70∘B110∘C140∘D80∘ABC is a cyclic triangle and the bisectors of ∠BAC,∠ABCand∠BCA meet the circle at P,Q and R respectively. Then the angle ∠RQP is:
A90∘−∠B2B90∘+∠B2C90∘+∠C2D90∘+∠B2
the triangle ABC,3A=2B and 2A=C. find the angles of the triangle
View SolutionThe distance of incentre of the right-angled triangle ABC (right angled at A) from B and C are √10and√5, respectively. The perimeter of the triangle is _____
View Solutionin a triangle ABC,C=3B=2(A+B) then find all the angles
View SolutionIn a triangle ABC, IF angle B is twice angle C then c (b +a) is equal to
View SolutionIn a triangle ABC, a = 2b and ∠A=3∠B. Which one of the following is correct ?
View Solution
