A graph between logt12 and log a (abscissa), a being the initial concentration of A in the reaction For reaction A→Product, the rate law is :
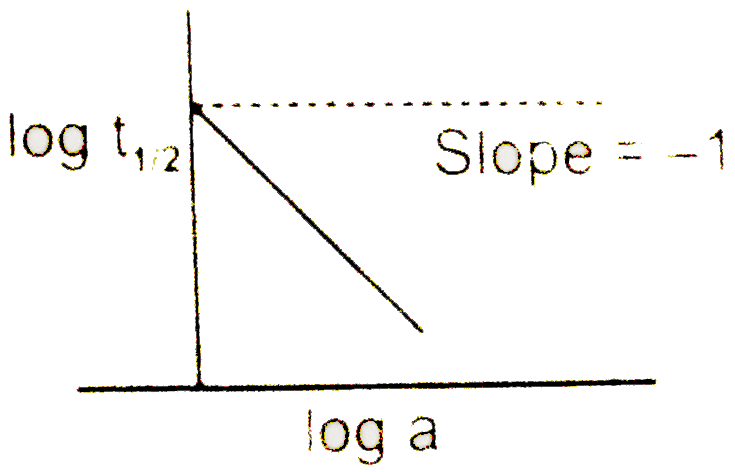
−d[A]dt=k
−d[A]dt=k[A]
−d[A]dt=k[A]2
−d[A]dt=k[A]3
The correct Answer is:C
t1/2=1k.a for 2nd order,
where a: initial conc. of reactant.
Topper's Solved these Questions
- CHEMICAL KINETICS BOOK - DISHA PUBLICATIONCHAPTER - CHEMICAL KINETICS EXERCISE - EXERCISE 1 : CONCEPT BUILDER (TOPICWISE)(TOPIC 3 : Theories of Rate of Reaction)
17 Videos
- CHEMICAL BONDING AND MOLECULAR STRUCTURE BOOK - DISHA PUBLICATIONCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTURE EXERCISE - EXERCISE-2: CONCEPT APPLICATOR
30 Videos
- CHEMISTRY IN EVERDAY LIFE BOOK - DISHA PUBLICATIONCHAPTER - CHEMISTRY IN EVERDAY LIFE EXERCISE - Exercise
88 Videos
Similar Questions
Following is the graph between logt1/2 and loga (a initial concentration) for a given reaction at 27∘C.

Find the order of reaction.
View SolutionFor a reaction A→ Products, a plot of logt12 ,versus log a is shown in figure. If the initial concentration of A is represented by a ,the order of the reaction is:-
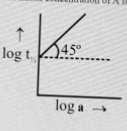
View Solution
Knowledge Check
A graph between log t1/2 and log a (abscissa), a being the initial concentration of A in the reaction A → product, is depicted in the figure. The rate law is
 A−d[A]dt=kB−d[A]dt=k[A]C−d[A]dt=k[A]2D−d[A]dt=k[A]3
A−d[A]dt=kB−d[A]dt=k[A]C−d[A]dt=k[A]2D−d[A]dt=k[A]3A graph between logt12 and log a (abscissa), a being the initial concentration of A in the reaction For reaction A→Product, the rate law is :
 A−d[A]dt=kB−d[A]dt=k[A]C−d[A]dt=k[A]2D−d[A]dt=k[A]3
A−d[A]dt=kB−d[A]dt=k[A]C−d[A]dt=k[A]2D−d[A]dt=k[A]3Following is the graph between logT50 and loga (a= initial concentration) for a given reaction at 27∘C. Hence order is
 A0B1C2D3
A0B1C2D3
Following is the graph between log T50 and log a (a = initial concentration) for a given reaction at 27∘C.
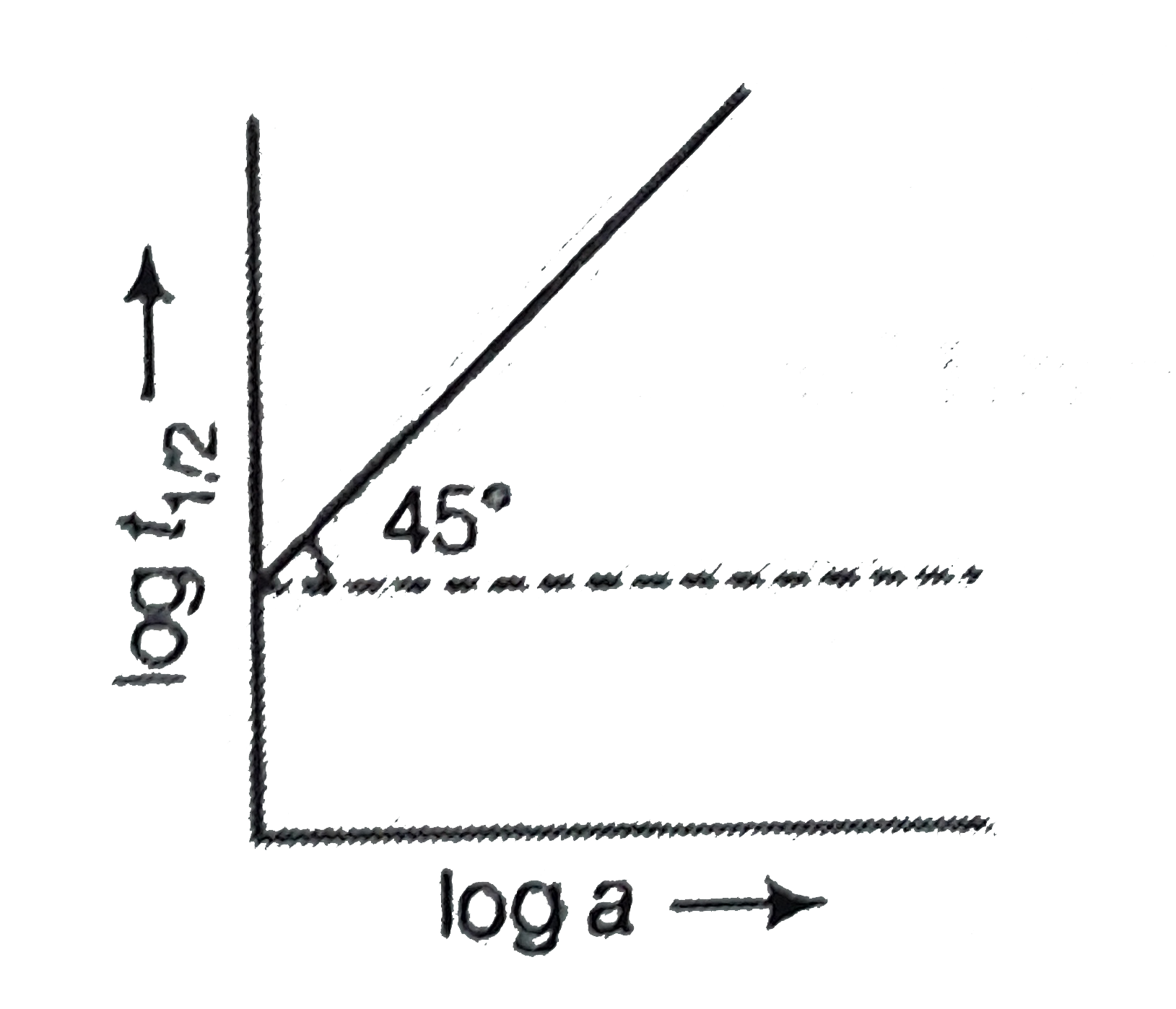
Hence, order is
View SolutionThe graph between log t1/2 and log a at a given temperature is
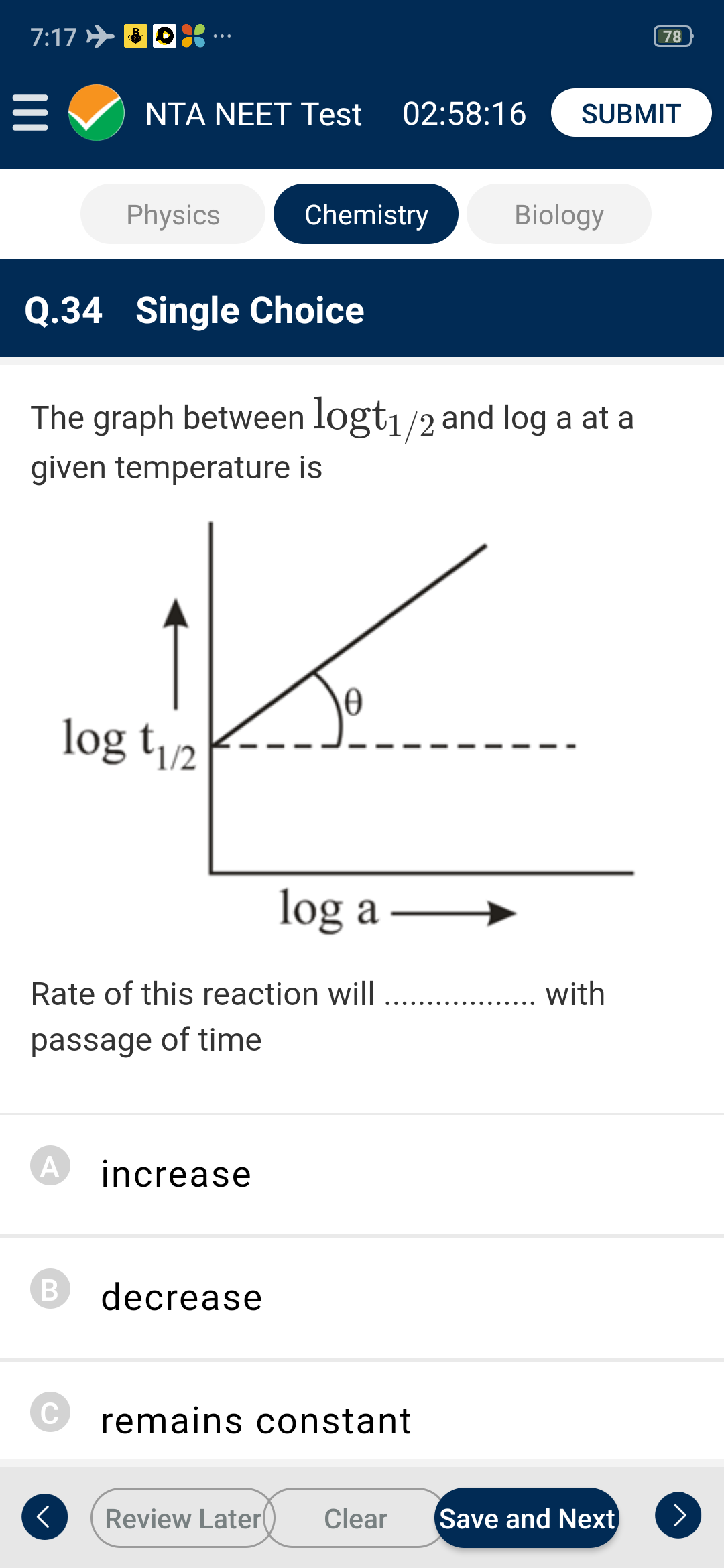
Rate of this reaction will …….with passage of time
View SolutionDerive an expression for the intergated rate equation for the first order reaction.
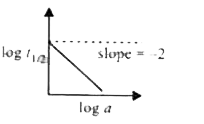
View SolutionPlotting log10t1/2 against log10[A0] (where A0 is the initial concentration of a reactant) for a fist order reaction the slope will be
View SolutionFor zero order reaction , t1/2 will be (A0 is the initial concentration , K is rate constant)
View Solution
