Two small balls having equal positive charge Q,C each are supended by two insulating strings of equal length L meter form a hook fixed to a stand . The whole set up is taken to a satellite in space where there is no gravity.Calculate the angle between the two strings and the tension in each string.
180∘,14πε0Q2(2L)2
90∘,14πε0Q2L2
180∘,14πε0Q22L2
180∘,14πε0Q2L2
The correct Answer is:A
In the absence of gravitational force, the only force acts on the spheres is electrostatic repulsion and so the angle between two suspension becomes 180∘ . So
F=14πε0Q2(2L)2 .
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - DISHA PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Exercise - 2 : Concept applicator
24 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - DISHA PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Exercise - 2 : Concept applicator
24 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - DISHA PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - EXERCISE -2 : CONCEPT ALLPLICATOR
30 Videos
- ELECTROMAGNETIC INDUCTION BOOK - DISHA PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - EXERCISE - 2 : Concept Applicator
29 Videos
Similar Questions
Two small balls having equal poistive charges Q( coulomb) on each are suspended by two insulating strings of equal length L(metre) from a hook fixed to a stand. The whole set up is taken in a satellite into space where there is no gravity (state of weightlessness). The angle between the two strings is...............and the tenison in each string is...................newtons.
View SolutionTwo identical balls having equal positive charge q coulomb are suspended by two in painting strings of equal length. What would be the effect on the force when a plastic sheet is inserted between the two?
View Solution
Knowledge Check
Two small balls having equal positive charge Q (coulomb) on each are suspended by two insulated string of equl length L meter, from a hook fixed to a stand. The whole set-up is taken in satellite into space where there is no gravity (state of weightlessness). Then the angle between the string and tension in the string is
 A180∘,14πε0.Q2(2L)2B90∘,14πε0.Q2L2C180∘,14πε0.Q22L2D180∘,14πε0.QL4L2
A180∘,14πε0.Q2(2L)2B90∘,14πε0.Q2L2C180∘,14πε0.Q22L2D180∘,14πε0.QL4L2Two small balls having equal positive charge Q (coulumb) on each suspended by two insulating strings of equal length L (metre) from a hook fixed to a stand. The whole set-up is taken in a satellite into space where there is no gravity (state of weightlessness). Then tension (newtons) in each string is:
AQ24π∈0L2BQ28π∈0L2CQ212π∈0L2DQ216π∈0L2Two small balls having equal positive charge Q(coulomb) on each are suspended by two insulated string of equal length L meter, from a hook fixed to a stand. The whole gravity (state of weightlessness). Then the angle between the string and tension in the string is
 A180∘,14πε0⋅Q2(2L)2B90∘,14πε0.Q2L2C180∘,14πε0.Q22L2D180∘,14πε0⋅Q24L2
A180∘,14πε0⋅Q2(2L)2B90∘,14πε0.Q2L2C180∘,14πε0.Q22L2D180∘,14πε0⋅Q24L2
Two small balls, each having charge q, are suspended by two insulating threads of equal length L fron a hook in an elevator. The elevator is freely falling. Calculate the angle etween the two threads and tension in each thread.
View SolutionTwo identical small bodies each of mass m and charge q are suspended from two strings each of length l from a fixed point. This whole system is taken into an orbiting artificial satellite, then find the tensio in strings
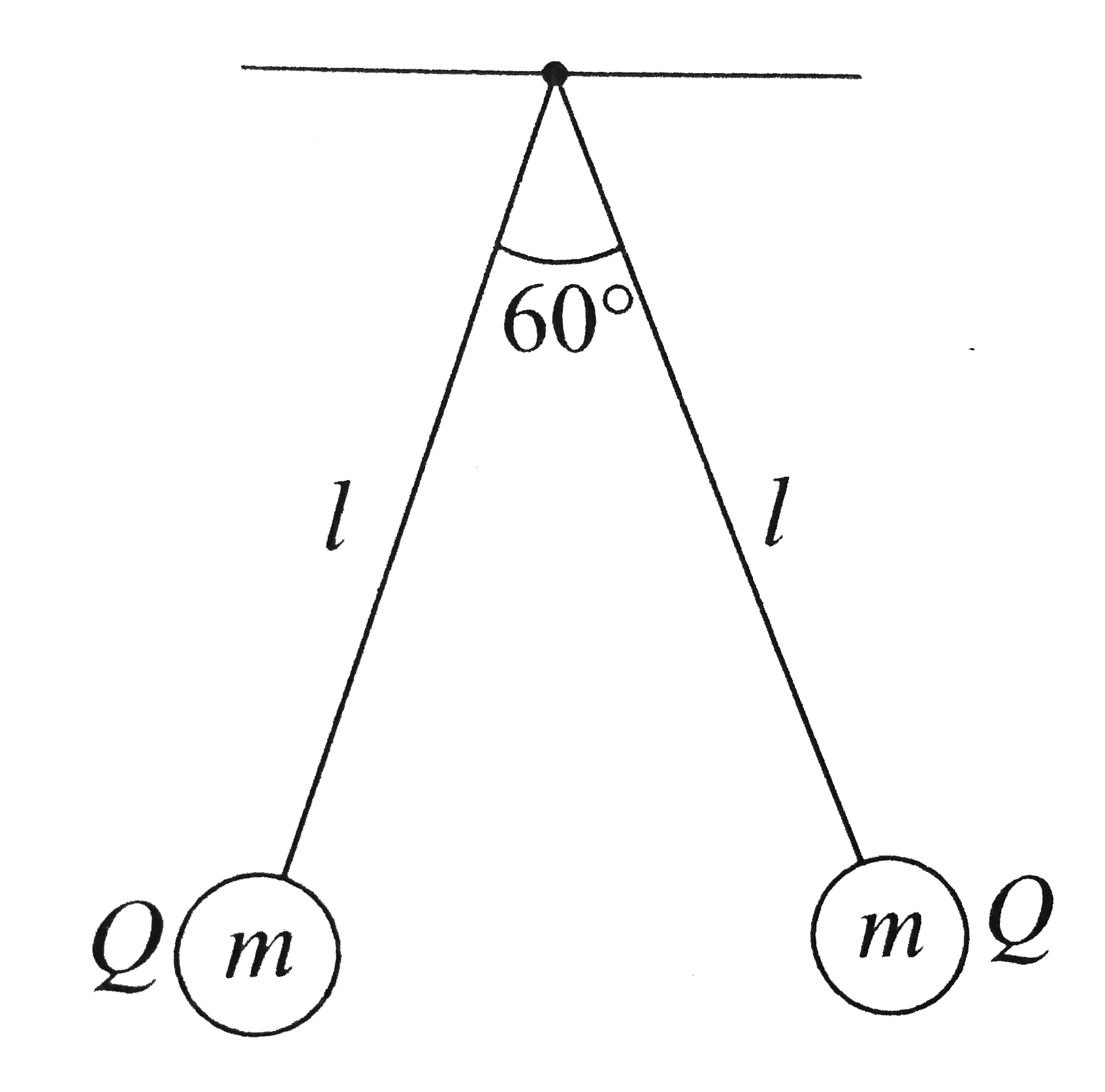
View SolutionTwo small balls, each having equal positive charge Q are suspended by two insulation strings of equal length l from a hook fixed to a stand. It mass of each ball =m and total angle between the two strings is 60∘m, then find the charge on each ball.
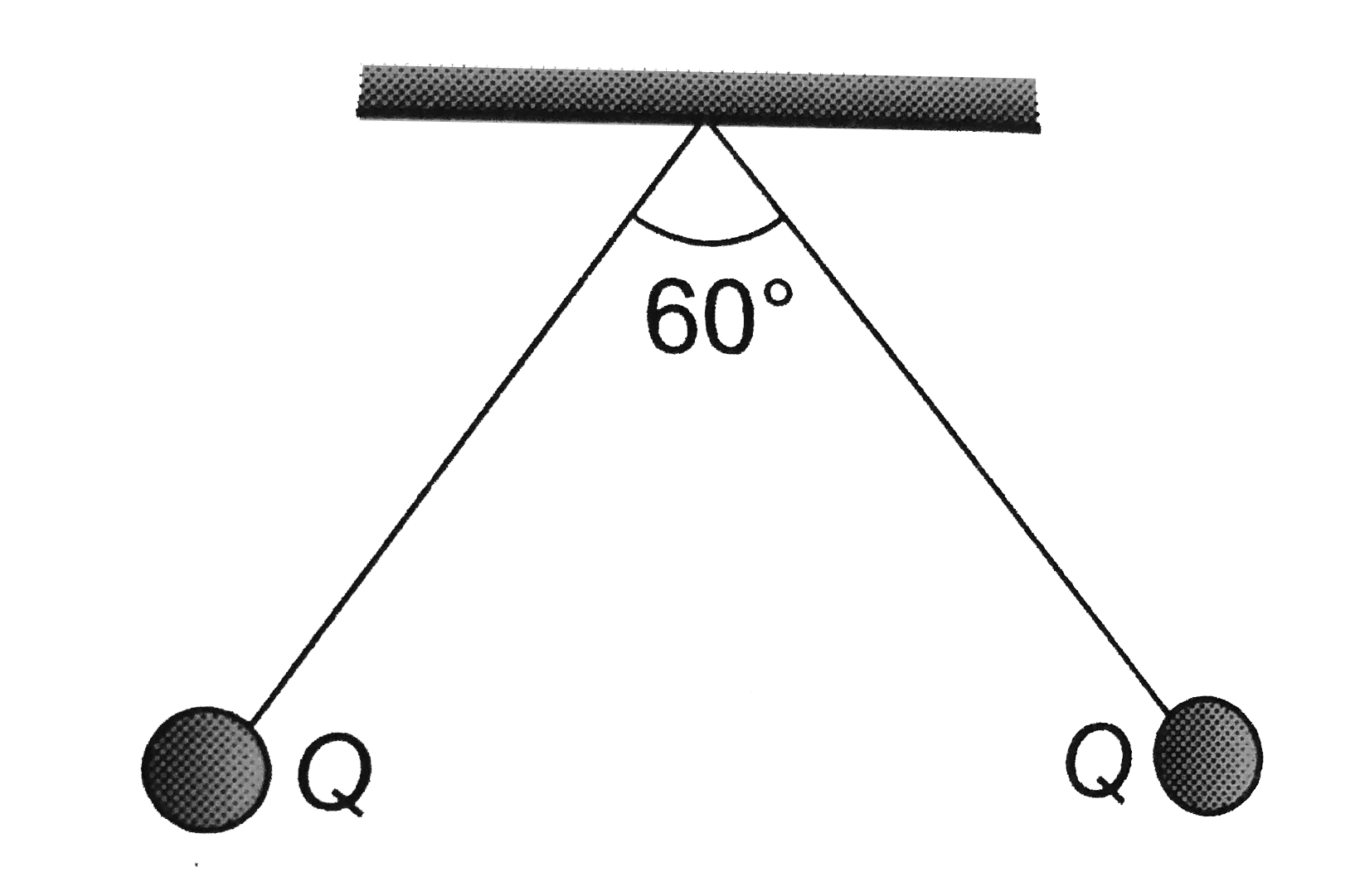
View SolutionTwo small spherical balls each carrying a charge Q=10μC( 10 micro=coulomb) are suspended by two insulating threads of equal lengths 1cm each, from a point fixed in the ceiling. It is found that in equilibrium threads are sepreated by an angle 60∘ between them, as shown in figure. What is the tension in the threads
(Given 14πε0=9×109Nm/C2 )
View SolutionTwo identical small bodies each of mass m and charge q are suspended from two strings each of length l from a fixed point. This whole system is taken into an orbiting artificial satellite, then find the tensio in strings
View Solution
