In each of the following questions, a series is given, with one term missing. Choose the correct alternative from the given ones that will complete the series.
20. 7, 2 = 59, 5, 3 = 28, 9, 1= 810, 2, 1 = 13, 5,4 = ?
19
9
20
239
The correct Answer is:A
7−2=5,7+2=9
⇒7,2=59
5−3=2,5+3=8
⇒5,3=28
9−1=8,9+1=10
⇒9,1=810
2−1=1,2+1=3
⇒2,1=13
Therefore,
5−3=1,5+4=9
⇒5,4=19
Similar Questions
In each of the following questions a series is given, with one term missing. Choose the correct alternatives from the given ones that will complete the series.
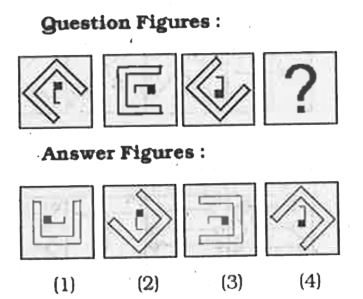 View Solution
View SolutionIn each of the following questions a series is given, with one term missing. Choose the correct alternatives from the given ones that will complete the series.
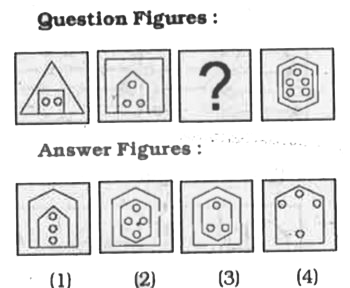 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In following questions, a series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.
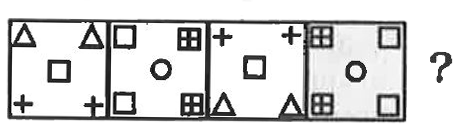 A
A B
B C
C D
D
- Question 2 - Select One
In following questions, a series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.
 A
A B
B C
C D
D
- Question 3 - Select One
In following questions, a series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.
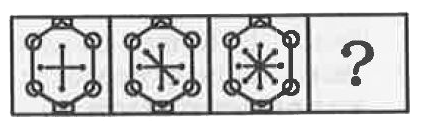 A
A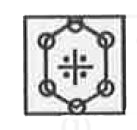 B
B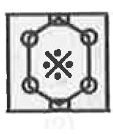 C
C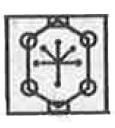 D
D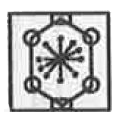
In following questions, a series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.
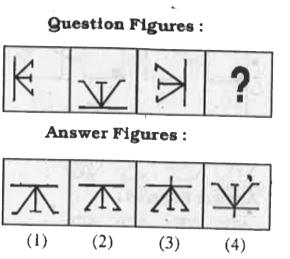 View Solution
View SolutionIn following questions, a series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.
 View Solution
View SolutionIn following questions, a series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.
 View Solution
View SolutionIn following questions, a series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.
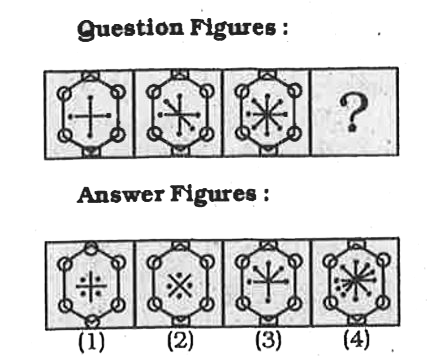 View Solution
View SolutionIn following questions, a series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.
 View Solution
View Solution
