The wave reaching the receiving antenna will have maximum intensity if the direct wave & wave after reflection from earth's surface
are out of phase by 90∘
are out of phase by 270∘
are in phase
None of these
The correct Answer is:A
To solve the problem of determining the condition under which the wave reaching the receiving antenna has maximum intensity when considering both the direct wave and the wave reflected from the Earth's surface, we can follow these steps:
1. Understanding Maximum Intensity:
- The maximum intensity at the receiving antenna occurs due to constructive interference between the direct wave and the reflected wave.
Hint: Remember that constructive interference happens when two waves combine to produce a wave of greater amplitude.
2. Condition for Constructive Interference:
- For constructive interference to occur, the path difference between the direct wave and the reflected wave must be an integer multiple of the wavelength (λ). This can be expressed mathematically as:
Path Difference=nλ(n=0,1,2,…)
Hint: Think about how waves interact when they meet: they can either add up (constructive) or cancel out (destructive).
3. Calculating Phase Difference:
- The phase difference (Δφ) corresponding to a path difference of λ is given by:
Δϕ=2πλ×Path Difference
- For a path difference of λ, we substitute:
Δϕ=2πλ×λ=2π
Hint: Remember that a phase difference of 2π means the waves are in phase.
4. Interpreting the Phase Difference:
- A phase difference of 2π indicates that the two waves are in phase, meaning they reach their maximum and minimum values at the same time.
Hint: Visualize the waves: if they start at the same point and move together, they are in phase.
5. Conclusion:
- Therefore, for maximum intensity at the receiving antenna, the direct wave and the reflected wave must be in phase.
Final Answer: The answer is "in phase".
- The maximum intensity at the receiving antenna occurs due to constructive interference between the direct wave and the reflected wave.
- For constructive interference to occur, the path difference between the direct wave and the reflected wave must be an integer multiple of the wavelength (λ). This can be expressed mathematically as:
Path Difference=nλ(n=0,1,2,…)
- The phase difference (Δφ) corresponding to a path difference of λ is given by:
Δϕ=2πλ×Path Difference
- For a path difference of λ, we substitute:
Δϕ=2πλ×λ=2π
- A phase difference of 2π indicates that the two waves are in phase, meaning they reach their maximum and minimum values at the same time.
- Therefore, for maximum intensity at the receiving antenna, the direct wave and the reflected wave must be in phase.
Topper's Solved these Questions
- COMMUNICATION SYSTEM Book:DISHA PUBLICATIONChapter:COMMUNICATION SYSTEM Exercise:EXERCISE-2 : Concept Applicator
Explore 30 Videos
- COMMUNICATION SYSTEM Book:DISHA PUBLICATIONChapter:COMMUNICATION SYSTEM Exercise:EXERCISE-2 : Concept Applicator
Explore 30 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBook:DISHA PUBLICATIONChapter:CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSExercise:CHAPTER 29 : (COMMUNICATION SYSTEMS)
Explore 15 Videos
- CONCEPT BUILDERBook:DISHA PUBLICATIONChapter:CONCEPT BUILDERExercise:Exercise-2 Concept Applicator
Explore 27 Videos
Similar Questions
Knowledge Check
The change in phase if a wave is reflected from a rigid surface is
AzeroBπ radianC2π radianDπ2 radianIntensities of the two waves of light are I and 4I. The maximum intensity of the resultant wave after superposition is
A(a) 5IB(b) 9IC(c) 16ID(d) 25ITwo waves of intensity I undergo interference. The maximum intensity obtained is
A(a) I/2B(b) IC(c) 2ID(d) 4I
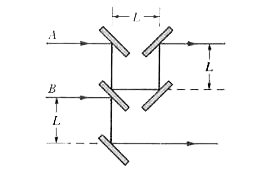
In Fig., sound waves A and B, both of wavelength λ , are initially in phase and traveling rightward, as indicated by the two rays. Wave A is reflected from four surfaces but ends up traveling in its original direction. Wave B ends in that direction after reflecting from two surfaces. Let distance L in the figure be expressed as a multiple q of λ:L=qλ. What are the (a) smallest and (b) third smallest values of q that put A and B exactly out of phase with each other after the reflections?
View SolutionRadio waves coming at ∠α to vetical are received by a radar after reflection from a nearby water surface and directly .what should be height of antenna from water surface so that it records a maximum intensity.(Wavelength =λ)
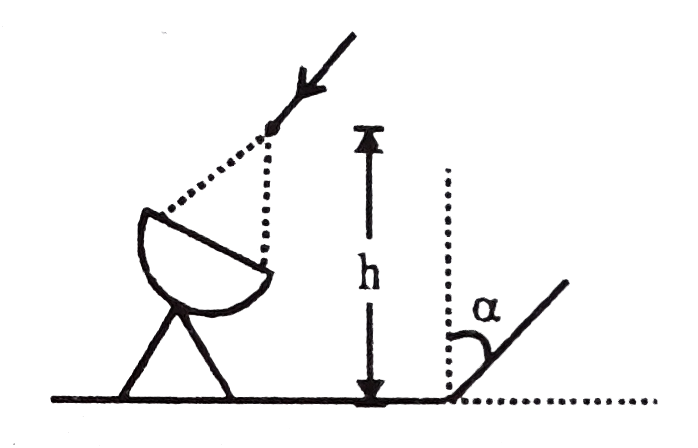
View SolutionA radio wave sent from the surface of the Earth reflects from the surface of the moon and returns to the Earth . The elapsed time between the generation of the wave and the detection of the reflected wave is .6444 s. Determine the distance from the surface of the Earth to the surface of the Moon .
Note: The speed of light is 2.9979×108 m/s
View SolutionAs a wave propagates
(i) the wave intensity remains constant for a plane wave
the wave intensity decreases as the inverse of the distance from the source for a spherical wave
(iii) the wave intensity decreases as the inverse square of the distance from the source for a spherical wave
(iv) total intensity of the spherical wave over the spherical surface centred at the source remains constant at all times
View SolutionWhen longitudinal waves are reflected from the surface of a rarer medium?
View Solution