2Ω,3Ω एवं 6Ω प्रतिरोध के तीन प्रतिरोधकों को श्रेणीक्रम में जोड़ा गया है। यदि 2Ω के प्रतिरोधकों में प्रवाहित धारा का परिणाम 1A है तो 6Ω के प्रतिरोधक मेंप्रवाहित होने वाली धारा का परिणाम होगा
2A
3A
1A
इनमें से कोई नहीं
1A
Topper's Solved these Questions
- प्रोयोगिकी Book:ALOK BHARTI PUBLICATIONChapter:प्रोयोगिकी Exercise:प्रयोग संख्या-5 (मौखिक प्रश्न एवं उनके उत्तर)
Explore 7 Videos
- प्रोयोगिकी Book:ALOK BHARTI PUBLICATIONChapter:प्रोयोगिकी Exercise:प्रयोग संख्या-5 (बहुविकल्पीय प्रश्न एवं उनके उत्तर)
Explore 4 Videos
- प्रोयोगिकी Book:ALOK BHARTI PUBLICATIONChapter:प्रोयोगिकी Exercise:प्रयोग संख्या-4 ( मौखिक प्रश्न एवं उनके उत्तर)
Explore 14 Videos
- प्रकाश - परावर्तन तथा अपवर्तन Book:ALOK BHARTI PUBLICATIONChapter:प्रकाश - परावर्तन तथा अपवर्तन Exercise:आंकिक प्रश्न एवं उत्तर
Explore 18 Videos
- मानव नेत्र तथा रंग - बिरंगा संसारBook:ALOK BHARTI PUBLICATIONChapter:मानव नेत्र तथा रंग - बिरंगा संसारExercise:आंकिक प्रश्न एवं उत्तर :
Explore 3 Videos
Similar Questions
समांतर क्रम संयोजन किसे कहते हैं?
View Solutionचित्र में A एवं B के बीच समतुल्य प्रतिरोध होगा
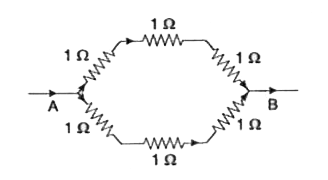
View Solutionश्रेणीक्रम संयोजन किसे कहते हैं?
View Solutionकोई अवतल दर्पण अपने सामने 10 cm दूरी पर रखें किसी बिंब का तीन गुना आवर्धित वास्तविक प्रतिबिंब बनाता है। प्रतिबिंब दर्पण से कितनी दूरी पर है?
View Solutionएक दीर्घ दृष्टिदोष युक्त नेत्र का निकट बिंदु 1m है | इस दोष को संशोधित करने के लिए आवश्यक लेंस की क्षमता क्या होगी ? यह मान लीजिए कि सामान्य नेत्र का निकट बिंदु 25 cm है |
View Solution283 v शिखर वोल्टता एवं 50HZ आवृति की एक ज्यावक्रीय वोल्टता एक श्रेणी बद्ध LCR परिपथ से जुडी है जिसमे R= 3Ω, L= 25.48mH एवं C= 796microfared है| ज्ञात कीजिये (a) परिपथ की प्रतिबाधा (b) स्रोत के सिरों के बीच लगी वोल्टता एवं परिपथ में प्रवाहित होने वाली धारा के बीच कालान्तर (c) परिपथ में होने वाला शक्ति क्षय (d) शक्ति गुणांक
माना कि पूर्व उदाहरण में वर्णित स्रोत की आवर्ती परिवर्तनशील है|(a) स्रोत कि किसी आवृति पर अनुनाद होगा| (b) अनुनाद की अवस्था में प्रतिबाधा, का धारा एवं क्षयित शक्ति की गणना कीजिए|
View Solutionयदि ω(≠1) इकाई का घनमूल हो तब ∣∣ ∣ ∣∣11+i+ω2ω21−i−1ω2−1−1−1+ω−i−1∣∣ ∣ ∣∣ बराबर है:
View Solutionयदि 1,ω,ω2 इकाई एक घनमूल हों, तो ∣∣∣1ωω−ω∣∣∣ का मान होगा -
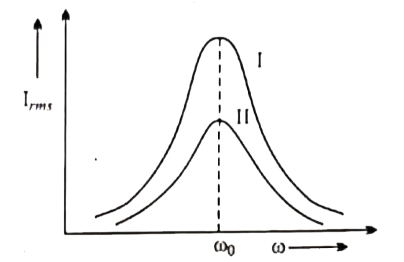
View Solutionदिए गए ग्राफ दो विभिन्न श्रेणी LCR परिपथों के लिए कोणीय आवृत्ति ω के साथ Irms धारा में होने वाले परिवर्तन को दर्शाते हैं। ग्राफों का सावधानीपूर्वक निरीक्षण कीजिए।
(i) जब दोनों परिपथों में धारा अधिकतम होती है, तो L और C के मानों में संबंध लिखिए।
(ii) उस परिपथ को संकेत कीजिए जिसमें- (a) शक्ति गुणांक अधिक है। तथा (b) गुणता कारक Q अधिक है।
प्रत्येक स्थिति के लिए कारण दीजिए।
View Solutionयदि omega इकाई का घनमूल हो तो ,सारणिक ∣∣ ∣ ∣∣1w3w2w31ww2w1∣∣ ∣ ∣∣ का गान ज्ञात कीजिये।
View Solutionयदि w इकाई का एक घनमूल हो तो सारणिक ∣∣ ∣ ∣∣1w4w8w4w81w81w4∣∣ ∣ ∣∣का मान है-
View Solutionयदि ω इकाई का एक घनमूल हो, तो सारणिक ∣∣ ∣ ∣∣1ω4ω8ω4ω81ω81ω4∣∣ ∣ ∣∣ का मान है-
View Solutionयदि ω इकाई का घनमूल हो तो सारणिक ∣∣ ∣ ∣∣1ωω2ωω21ω21ω∣∣ ∣ ∣∣ का मान ज्ञात कीजिए |
View Solutionयदि ω इकाई का एक काल्पनिक घन मूल है, तो सारणिक ∣∣ ∣ ∣∣1+ωω2−ω1+ω2ω−ω2ω+ω2ω−ω2∣∣ ∣ ∣∣ का मान है-
View Solutionयदि ω(≠1) इकाई का घनमूल है और (1+ω)7=A+Bω हो, तो A और B क्रमशः होंगे
View Solutionमाना ω एक सम्मिश्र संख्या ऐसी है कि 2ω+1=z जहाँ, z=√−3 है। यदि ∣∣ ∣ ∣∣1111−ω2−1ω21ω2ω2∣∣ ∣ ∣∣=3k है तो k बराबर है
View Solution

