What is the electric potential at point P, located at the center of the square of charged particles shown in Fig. 24-16a? The distanced is 1.3 m, and the charges are
q1=+12nC, q3=+31nC,
q2=−24nC, q4=+17nC.
To find the electric potential at point P, located at the center of the square formed by the charged particles, we can follow these steps:
Step 1: Identify the Charges and Their Values
The charges are given as:
- q1=+12nC
- q2=−24nC
- q3=+31nC
- q4=+17nC
Step 2: Calculate the Distance from Each Charge to Point P
The distance d between the charges and point P is given as 1.3m. However, since point P is at the center of the square, the distance from each charge to point P is A, where A=d√2 because the distance from the center to the corner of a square is given by the formula a√2.
Calculating A:
A=1.3√2≈0.919m
Step 3: Use the Formula for Electric Potential
The electric potential V due to a point charge is given by:
V=kQr
where k is Coulomb's constant (k≈9×109N m2/C2), Q is the charge, and r is the distance from the charge to the point where the potential is being calculated.
Step 4: Calculate the Total Electric Potential at Point P
Since electric potential is a scalar quantity, we can sum the potentials due to each charge at point P:
VP=V1+V2+V3+V4
Substituting the values:
VP=k(q1A+q2A+q3A+q4A)
Factoring out k and A:
VP=k1A(q1+q2+q3+q4)
Step 5: Calculate the Total Charge
Now, we calculate the total charge:
qtotal=q1+q2+q3+q4=12nC−24nC+31nC+17nC=36nC=36×10−9C
Step 6: Substitute Values into the Potential Equation
Now substitute k, A, and qtotal into the equation:
VP=9×109(36×10−90.919)
Step 7: Calculate the Electric Potential
Calculating the value:
VP≈9×109×36×10−90.919≈350V
Final Answer
The electric potential at point P is approximately 350V.
---
The charges are given as:
- q1=+12nC
- q2=−24nC
- q3=+31nC
- q4=+17nC
The distance d between the charges and point P is given as 1.3m. However, since point P is at the center of the square, the distance from each charge to point P is A, where A=d√2 because the distance from the center to the corner of a square is given by the formula a√2.
A=1.3√2≈0.919m
The electric potential V due to a point charge is given by:
V=kQr
where k is Coulomb's constant (k≈9×109N m2/C2), Q is the charge, and r is the distance from the charge to the point where the potential is being calculated.
Since electric potential is a scalar quantity, we can sum the potentials due to each charge at point P:
VP=V1+V2+V3+V4
Substituting the values:
VP=k(q1A+q2A+q3A+q4A)
Factoring out k and A:
VP=k1A(q1+q2+q3+q4)
Now, we calculate the total charge:
qtotal=q1+q2+q3+q4=12nC−24nC+31nC+17nC=36nC=36×10−9C
Now substitute k, A, and qtotal into the equation:
VP=9×109(36×10−90.919)
Calculating the value:
VP≈9×109×36×10−90.919≈350V
The electric potential at point P is approximately 350V.
Topper's Solved these Questions
- ELECTRIC POTENTIALBook:RESNICK AND HALLIDAYChapter:ELECTRIC POTENTIALExercise:SAMPLE PROBLEM 24.08 Potential is not a vector, orientation is irrelevant
Explore 1 Video
- ELECTRIC POTENTIALBook:RESNICK AND HALLIDAYChapter:ELECTRIC POTENTIALExercise:SAMPLE PROBLEM 24.09 Net potential due to two charged particles
Explore 1 Video
- ELECTRIC POTENTIALBook:RESNICK AND HALLIDAYChapter:ELECTRIC POTENTIALExercise:SAMPLE PROBLEM 24.06 Finding the potential
Explore 1 Video
- ELECTRIC CHARGES AND FIELDSBook:RESNICK AND HALLIDAYChapter:ELECTRIC CHARGES AND FIELDSExercise:Practice Questions (Integer Type )
Explore 3 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESNICK AND HALLIDAYChapter:ELECTROMAGNETIC INDUCTIONExercise:PRACTICE QUESTIONS (Integer Type)
Explore 14 Videos
Similar Questions
Four point charges Q , q Q and q are placed at the corners of a square of side 'a' as shown in the Fig. Find the
resultant electric force on a charge Q
View SolutionFour point charges Q.q Q and q are placed at the corners of a square side 'a' as shown in the figures.

Find the resultant electric force on a charge Q,
View Solution
Knowledge Check
What is the electric potential at a distance of 9 cm from 3 nC?
A270 VB3 VC300 VD30 VA particle carrying charge + q is held at the center of a square of each side arranged on the square as shown in Fig. If q = 2 muC, what is the net force on the particle?
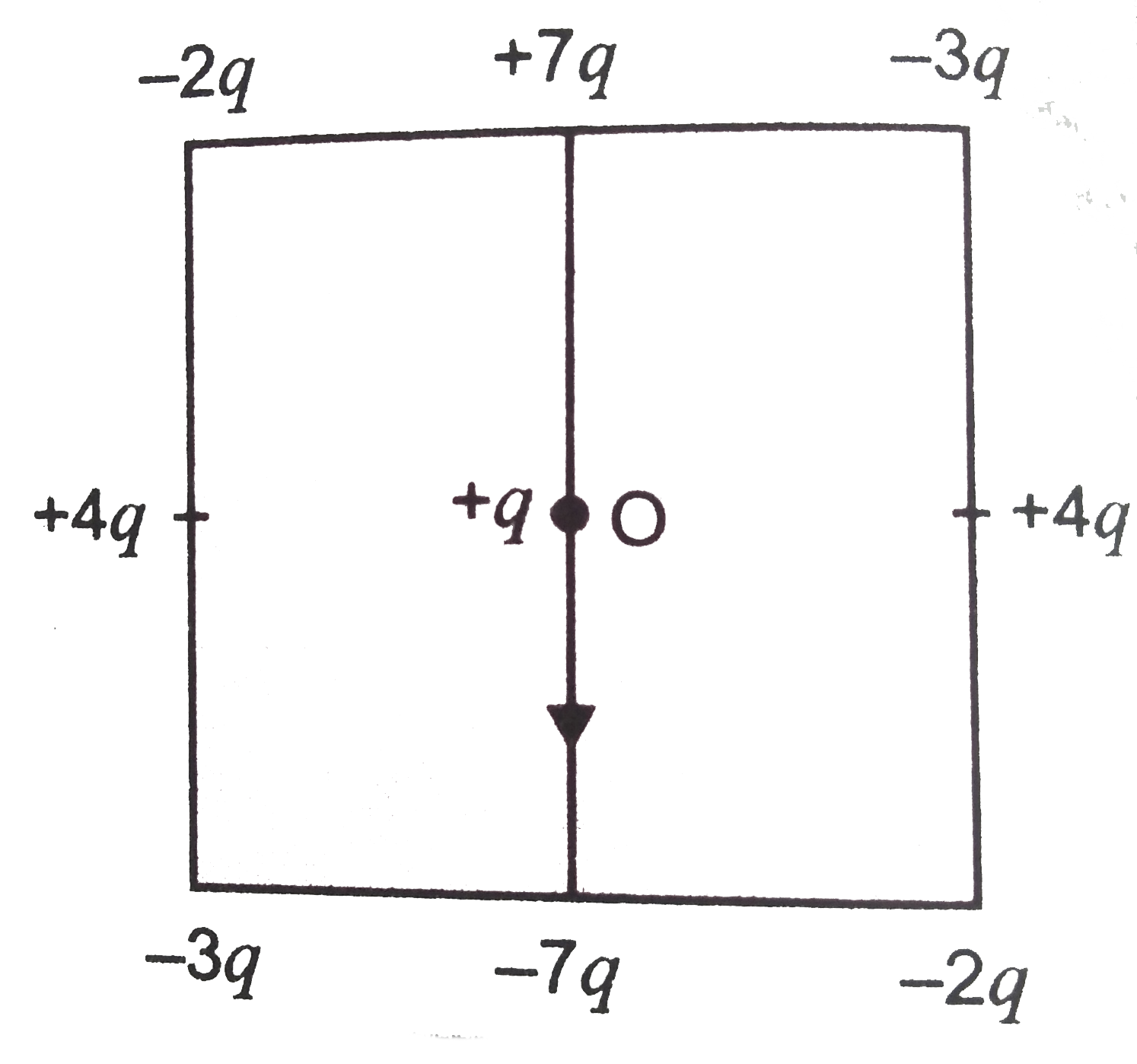 A36×14×4×10−3NB16×14×4×10−3NC26×14×4×10−3ND6×14×4×10−3N
A36×14×4×10−3NB16×14×4×10−3NC26×14×4×10−3ND6×14×4×10−3NThe value of charge q1,q2andq3 as shown in the figure are
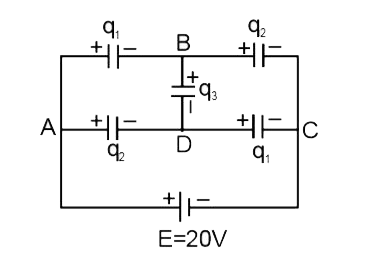 Aq1=32μC,q2=24μC,q3=−8μCBq1=48μc,q2=16μC,q3=+8μCCq1=32μC,q2=24μC,q3=+8μCDq1=3μC,q2=4μC,q3=+2μC
Aq1=32μC,q2=24μC,q3=−8μCBq1=48μc,q2=16μC,q3=+8μCCq1=32μC,q2=24μC,q3=+8μCDq1=3μC,q2=4μC,q3=+2μC
Four point charges Q , q Q and q are placed at the corners of a square of side 'a' as shown in the Fig. Find the
potential energy of this system .
View SolutionThe electric lines of force of two point charges are shown in fig. What is the value of the ratio q1/q2 ?

View SolutionCharges q,2q,3q and 4q are placed at the corners A,B,C and D of a square as shown in the following figure. The directon of electric field at the centre of the square is along

View SolutionElectric charges -q -q -q and 3q are placed at the corners of a square ABCD of length 1 as shown in figure.The magnitude of electric dipole moment of the system is
View SolutionThe electric potential at a point certain distance from a point charge is 600 V and the electric field is 200NC−1. Which of the following statements will be true?
View Solution