The cycle of a petrol engine can be approximated by an Otto cycle (Fig. 21-20a). 1→ 2 and 3 → 4 are adiabatic compression and expansion, respectively, 2 →3 and 4→1 are constant-volume processes. Treat the working medium as an ideal gas with constant γ=Cp/Cv, Compute the efficiency of this cycle for g = 1.4 and compression ratio, r=Vi/Vf=10

We can see from the p-V graph (Fig. 21-20b) that it is a cyclic process as the working medium returns to its initial state. We can see from the p-V graph that in the process 3→ 4, the engine is doing positive work on the surroundings and in 1 → 2, it is doing negative work as the gas is compressed. In other two processes, 2→ 3 and 4 → 1, work done is zero, as ΔV =0.
The efficiency of a cyclic process is given by ε=W/Q1, where W is the work done by the cycle and Q1 is the amount of heat absorbed by the working medium in this case, gas). Because the working medium returns to its initial state W=Q1−Q2, whereQ2 is the amount of heat transferred from the gas. Therefore,
ε=Q1−Q2Q1=1−Q2Q1
As the processes 1→ 2 and 3 →4 are adiabatic, heat transfer can take place only during the 2→ 3 and 1 →4 stages.
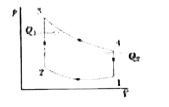
Calculations: Let us calculate Q1 and Q2 Since both processes are occurring at a constant volume (Fig. 21-20b), we may write
Q1=∫32dQ=Cv∫32dT=Cv(T3−T2)
Q2=CV∫34dT=−Cv(T1−T4)=Cv(T4−T1)
and Q2Q1=T4−T1T3−T2
We know that for an adiabatic process
pVγ = constant or TVr−1= constant
So _1Vγ−1i=T2Vγ−1f
T3Vr−1f−T4Vγ−1f
Dividing Eq. 21-49 by Eq. 21-48, we get
T4T1=T3T2
Subtracting 1 from both sides and solving, gives
T4−T1T1=T3−T2T2
Rearranging above relation and using Eq. 21-48 gives
T3−T1T3−T2=T1T2=(Vf)(Vi)γ−1
and therefore, the efficiency is
ε=1−(1r)γ−1
For γ = 1.4 and r= 10, the efficiency is
ε=1−(0.10)0.4=0.6=60%
The maximum possible efficiency, if the cycle would have been Carnot cycle, would be,1−T2/T4, as T2 and T4 are the lowest and highest temperatures in the cycle. It can be seen that efficiency is less than the Carnot efficiency as the value of T1/T2, would be more than Т_2 //T_4
Topper's Solved these Questions
- THE FIRST LAW OF THERMODYNAMICSBOOK - RESNICK AND HALLIDAYCHAPTER - THE FIRST LAW OF THERMODYNAMICSEXERCISE - CHECK POINT
8 Videos
- THE FIRST LAW OF THERMODYNAMICSBOOK - RESNICK AND HALLIDAYCHAPTER - THE FIRST LAW OF THERMODYNAMICSEXERCISE - PROBLEMS
41 Videos
- TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (Integer Type)
4 Videos
- THE KINETIC THEORY OF GASESBOOK - RESNICK AND HALLIDAYCHAPTER - THE KINETIC THEORY OF GASESEXERCISE - PRACTICE QUESTIONS
72 Videos
Similar Questions
If Cp and Cv are molar heats at constant pressure and constant volume respectively and R is gas constant for 1 mole, then the correct relation is
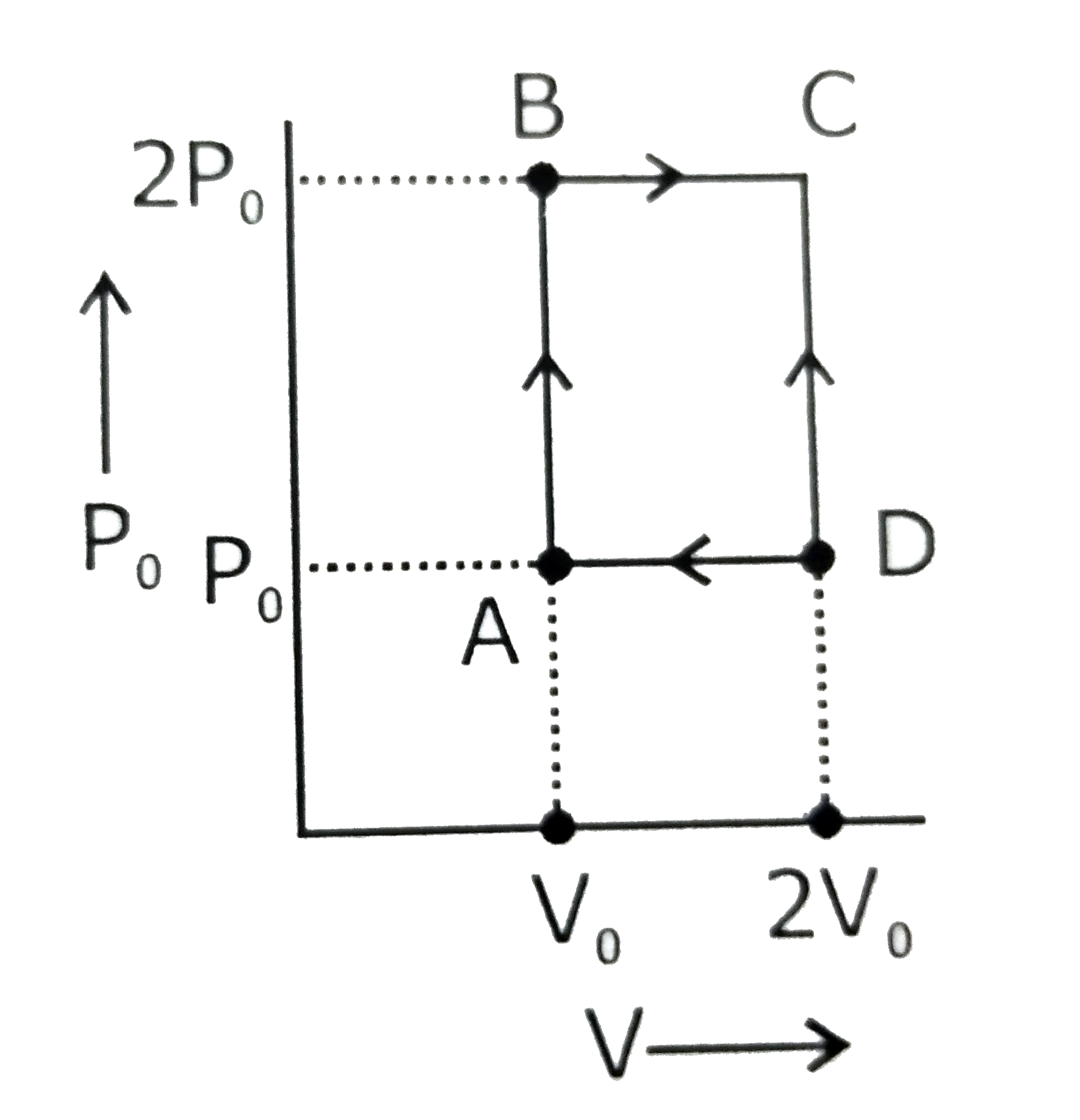
View SolutionAn engine operates by taking n moles of an ideal gas through the cycle ABCDA shown in figure. The thermal efficiency of the engine is -(Take Cv = 15.R, where R is gas constant)
View Solution
Knowledge Check
Initial pressure and volume of a gas are P and V respectively. First its volume is expanded to 4V by isothermal process and then again its volume makes to be V by adiabatic process then its final pressure is (γ=1.5) -
A8PB4PCPD2PThe molar specific heat of an ideal gas at constant pressure and constant volume is Cp and Cv respectively. If R is the universal gas constant and the ratio of Cp to Cv is γ, then Cv.
A1−γ1+γB1+γ1−γCγ−1RDRγ−1For a gas if γ=1.4 , then atomically, Cp and Cv of the gas are respectively
AMonatomic, 52R,32RBMonatomic, 72R,52RCDiatomic, 72R,52RDTriatomic, 72R,52R
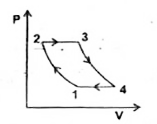
A gas undergoes cyclic process 1-2-3-4-1 in which 1-2 and 3-4 are adiabatic process 2-3 and 4-1 are isobaric process. If P2P1=k then what will be the efficiency of cycle in terms of k and γ where γ=Cp/Cv.
View SolutionThe efficiency of otto cycle for petrol engine is 50% and the adiabatic constant is 1.4. calculate the compression ratio.
View SolutionHow much heat energy is required to do 10 kWh of work by a petrol engine, whose adiabatic compression ratio is 10 ? Given γ=1.4
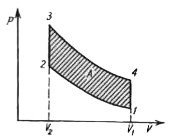
View SolutionFigure depicts an idealized cycle of a petrol internal combustion engine. The segment 1-2 corresponds to the adiabatic compression of the combustible mixture, segment 2-3, to the isochoric combustion of fuel in the course of which the working fluid receives an amount of heat Q, segment 3-4 corresponds to the adiabatic expansion of the working fluid, segment 4-1, to the isochoric exhaust of spent gases. Express the engine's efficiency in terms of the gas compression ratio x=V2/V1.
View SolutionDuring an adiabatic process of an ideal gas, if P is proportional to 1V1.5, then the ratio of specific heat capacities at constant pressure to that at constant volume for the gas is
View Solution
