A steel string guitar is strung so that there is negligible tension in the strings at a temperature of 24.9∘C . The guitar is taken to an outdoor winter concert where the temperature of the string decrease to −15.1∘C . The cross-sectional area of a particular string is 5.5×10−6m2 . The distance between the points where the string is attached does not change . For steel , Young's modulus is 2.0×1011N/m2 , and the coefficient of linear expansion is 1.2×10−5/∘C . Use your knowledge of liner thermal expansion and stress to calculate the tension in the string at the concert.
530 N
240 N
120 N
60 N
The correct Answer is:A
To solve the problem of calculating the tension in the steel string of a guitar when the temperature changes, we can follow these steps:
1. Identify the Initial and Final Temperatures:
- Initial temperature T1=24.9∘C
- Final temperature T2=−15.1∘C
2. Calculate the Change in Temperature:
ΔT=T2−T1=−15.1−24.9=−40.0∘C
3. Identify the Given Values:
- Cross-sectional area A=5.5×10−6m2
- Young's modulus E=2.0×1011N/m2
- Coefficient of linear expansion α=1.2×10−5/∘C
4. Calculate the Strain:
The strain ϵ due to the temperature change can be calculated using the formula:
ϵ=αΔT
Substituting the values:
ϵ=(1.2×10−5)×(−40)=−4.8×10−4
5. Calculate the Stress:
Stress σ is related to strain and Young's modulus by:
σ=E⋅ϵ
Substituting the values:
σ=(2.0×1011)×(−4.8×10−4)=−9.6×107N/m2
6. Calculate the Tension:
The tension T in the string can be calculated using the formula:
T=σ⋅A
Substituting the values:
T=(−9.6×107)×(5.5×10−6)=−528N
Since tension is a force, we take the absolute value:
T≈530N
Final Answer:
The tension in the string at the concert is approximately 530 N.
- Initial temperature T1=24.9∘C
- Final temperature T2=−15.1∘C
ΔT=T2−T1=−15.1−24.9=−40.0∘C
- Cross-sectional area A=5.5×10−6m2
- Young's modulus E=2.0×1011N/m2
- Coefficient of linear expansion α=1.2×10−5/∘C
The strain ϵ due to the temperature change can be calculated using the formula:
ϵ=αΔT
Substituting the values:
ϵ=(1.2×10−5)×(−40)=−4.8×10−4
Stress σ is related to strain and Young's modulus by:
σ=E⋅ϵ
Substituting the values:
σ=(2.0×1011)×(−4.8×10−4)=−9.6×107N/m2
The tension T in the string can be calculated using the formula:
T=σ⋅A
Substituting the values:
T=(−9.6×107)×(5.5×10−6)=−528N
Since tension is a force, we take the absolute value:
T≈530N
The tension in the string at the concert is approximately 530 N.
Topper's Solved these Questions
- TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION Book:RESNICK AND HALLIDAYChapter:TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION Exercise:PRACTICE QUETIONS (More than One Correct Choice Type )
Explore 7 Videos
- TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION Book:RESNICK AND HALLIDAYChapter:TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION Exercise:PRACTICE QUETIONS (Matrix- Match )
Explore 3 Videos
- TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION Book:RESNICK AND HALLIDAYChapter:TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION Exercise:PROBLEMS
Explore 24 Videos
- RIGID BODY DYNAMICS-IIBook:RESNICK AND HALLIDAYChapter:RIGID BODY DYNAMICS-IIExercise:PRACTICE QUESTIONS (Integer Type)
Explore 2 Videos
- THE FIRST LAW OF THERMODYNAMICSBook:RESNICK AND HALLIDAYChapter:THE FIRST LAW OF THERMODYNAMICSExercise:PRACTICE QUESTIONS ( INTEGER TYPE )
Explore 3 Videos
Similar Questions
Knowledge Check
A string has tension T. For tripling the frequency. The tension is string will become
A3TBT9CT√3D9TA mass M is hung with a light inextensible string. Tension in horizontal part of string is.
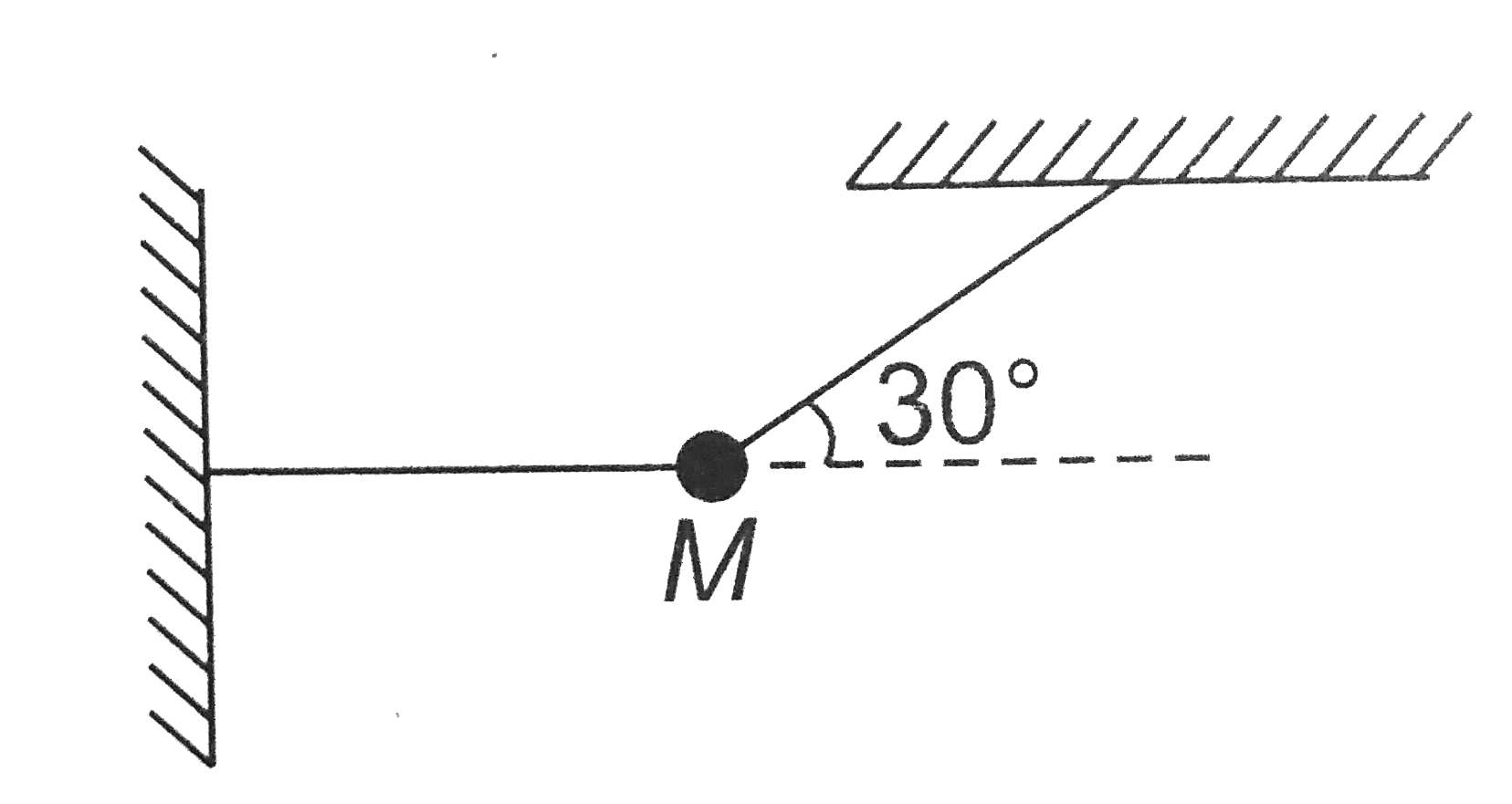 A√3MgB√2MgCmg√3Dmg2
A√3MgB√2MgCmg√3Dmg2When we tighten the string on a guitar, its pitch
AIncreasesBDecreasesCRemains sameDMay increase or decrease
A 5.5 m length of string has a mass of 0.035 kg. If the tension in the string is 77 N the speed of a wave on the string is
View SolutionA string of 7 m length has a mass of 0.035 kg. If tension in the string is 60.5 N, then speed of a wave on the string is :
View SolutionA 5.5 m length of string has a mass of 0.035 kg. If the tension in the string is 77 N the speed of a wave on the string is
View SolutionA string of 7 m length has a mass of 0.035 kg. If tension in the string is 60.5 N. Then speed of a wave on the string is
View SolutionA string of 7 m length has a mass of 0.035 kg. If tension in the string is 60.5 N, then speed of a wave on the string is
View Solution