Block 1, with mass m1 and speed 3.0 m/s, slides along an x axis on a frictionless floor and then undergoes a one dimensional elastic collision with stationary block 2, with mass m2=0.40m1. The two blocks then slide into a region where the coefficient of kinetic friction is 0.50, there they stop. How far into that region do (a) block 1 and (b) block 2 slide?
The correct Answer is:(a)d1=0.1698 m ≈ 17cm ; (b) d2= 1.878 m ≈ 1.9 m
To solve the problem step by step, we need to analyze the elastic collision and the motion of the blocks after the collision.
Step 1: Understand the initial conditions
- Block 1 has mass m1 and initial speed u1=3.0m/s.
- Block 2 has mass m2=0.40m1 and is initially at rest, so u2=0m/s.
Step 2: Apply conservation of momentum
For a one-dimensional elastic collision, the conservation of momentum states:
m1u1+m2u2=m1v1+m2v2
Substituting the known values:
m1(3.0)+0.40m1(0)=m1v1+0.40m1v2
This simplifies to:
3.0m1=m1v1+0.40m1v2
Dividing through by m1:
3.0=v1+0.40v2(1)
Step 3: Apply conservation of kinetic energy
For elastic collisions, kinetic energy is also conserved:
12m1u21+12m2u22=12m1v21+12m2v22
Substituting the known values:
12m1(3.0)2+0=12m1v21+12(0.40m1)v22
This simplifies to:
4.5m1=12m1v21+0.20m1v22
Dividing through by m1:
4.5=12v21+0.20v22(2)
Step 4: Solve the system of equations (1) and (2)
From equation (1):
v1=3.0−0.40v2
Substituting v1 into equation (2):
4.5=12(3.0−0.40v2)2+0.20v22
Expanding and simplifying:
4.5=12(9−2.4v2+0.16v22)+0.20v22
4.5=4.5−1.2v2+0.08v22+0.20v22
0=−1.2v2+0.28v22
Rearranging gives:
0.28v22−1.2v2=0
Factoring out v2:
v2(0.28v2−1.2)=0
Thus, v2=0 or v2=1.20.28≈4.29m/s.
Step 5: Calculate v1
Substituting v2 back into equation (1):
v1=3.0−0.40(4.29)≈1.28m/s
Step 6: Calculate the distance each block slides
The frictional force acting on each block is given by:
Ff=μmg
Where μ=0.5 and g≈9.8m/s2. Thus:
Ff=0.5m1g
The deceleration a due to friction is:
a=Ffm=μg=0.5×9.8≈4.9m/s2
Using the equation of motion v2=u2+2as, where v=0:
1. For Block 1:
0=(1.28)2−2(4.9)s1⟹s1=(1.28)22×4.9≈0.083m
2. For Block 2:
0=(4.29)2−2(4.9)s2⟹s2=(4.29)22×4.9≈1.87m
Final Answers:
- (a) Block 1 slides approximately 0.083m.
- (b) Block 2 slides approximately 1.87m.
- Block 1 has mass m1 and initial speed u1=3.0m/s.
- Block 2 has mass m2=0.40m1 and is initially at rest, so u2=0m/s.
For a one-dimensional elastic collision, the conservation of momentum states:
m1u1+m2u2=m1v1+m2v2
Substituting the known values:
m1(3.0)+0.40m1(0)=m1v1+0.40m1v2
This simplifies to:
3.0m1=m1v1+0.40m1v2
Dividing through by m1:
3.0=v1+0.40v2(1)
For elastic collisions, kinetic energy is also conserved:
12m1u21+12m2u22=12m1v21+12m2v22
Substituting the known values:
12m1(3.0)2+0=12m1v21+12(0.40m1)v22
This simplifies to:
4.5m1=12m1v21+0.20m1v22
Dividing through by m1:
4.5=12v21+0.20v22(2)
From equation (1):
v1=3.0−0.40v2
Substituting v1 into equation (2):
4.5=12(3.0−0.40v2)2+0.20v22
Expanding and simplifying:
4.5=12(9−2.4v2+0.16v22)+0.20v22
4.5=4.5−1.2v2+0.08v22+0.20v22
0=−1.2v2+0.28v22
Rearranging gives:
0.28v22−1.2v2=0
Factoring out v2:
v2(0.28v2−1.2)=0
Thus, v2=0 or v2=1.20.28≈4.29m/s.
Substituting v2 back into equation (1):
v1=3.0−0.40(4.29)≈1.28m/s
The frictional force acting on each block is given by:
Ff=μmg
Where μ=0.5 and g≈9.8m/s2. Thus:
Ff=0.5m1g
The deceleration a due to friction is:
a=Ffm=μg=0.5×9.8≈4.9m/s2
1. For Block 1:
0=(1.28)2−2(4.9)s1⟹s1=(1.28)22×4.9≈0.083m
0=(4.29)2−2(4.9)s2⟹s2=(4.29)22×4.9≈1.87m
- (a) Block 1 slides approximately 0.083m.
- (b) Block 2 slides approximately 1.87m.
Topper's Solved these Questions
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Single Correct Choice )
47 Videos
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (More than One Correct Choice)
5 Videos
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )
4 Videos
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTION (INTEGER TYPE)
3 Videos
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)
3 Videos
Similar Questions
In Fig. , block 1 of mass m1 slides from rest along a frictionless ramp from height h = 3.00 m and then collides with stationary block 2, which has mass m2=2.00m1. After the collision, block 2 slides into a region where the coefficient of kinetic friction μk is 0.450 and comes to a stop in distance d within that region. What is the value of distance d if the collision is (a) elastic and (b) completely inelastic?

View SolutionBlock 1 of mass m1 slides along a frictionless floor and into a one-dimensional elastic collision with stationary block 2 of mass m2=3m1. Prior to the collision, the center of mass of the two block system had a speed of 3.00 m/s. Afterward, what are the speeds of (a) the center of mass and (b) block 2 ?
View Solution
Knowledge Check
A block of mass M is sliding down the plane. Coefficient of static friction is μs and kinetic friction is μk. Then friction force acting on the block is :
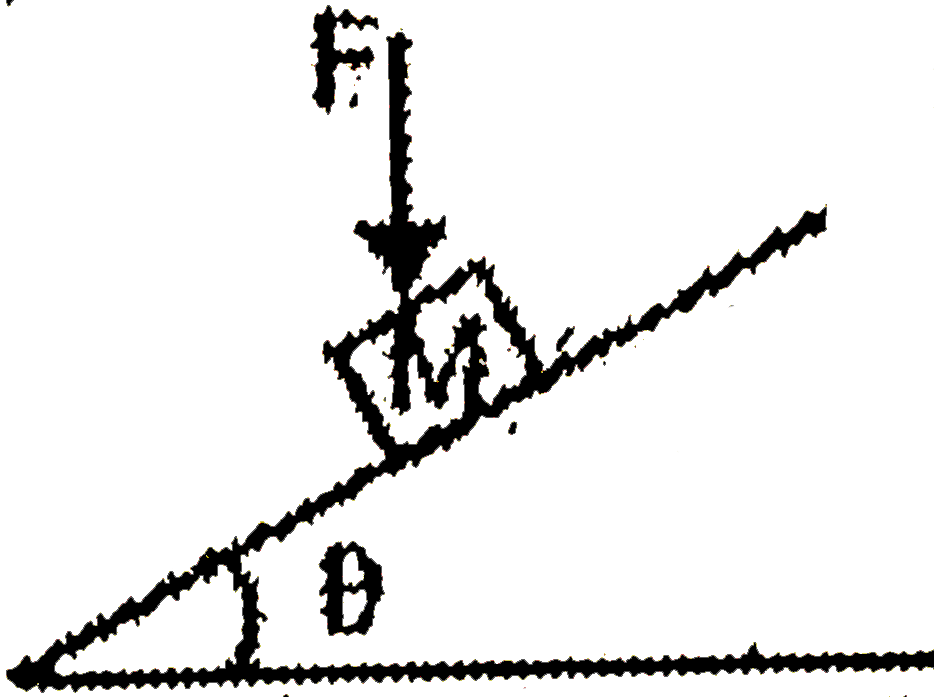 A(F+Mg)sinθBμk(F+Mg)cosθCμsMgcosθD(Mg+F)sinθ
A(F+Mg)sinθBμk(F+Mg)cosθCμsMgcosθD(Mg+F)sinθBlock A of mass M in the system shown in the figure slides down the incline at a constant speed. The coefficient of friction between block A and the surface is 1 3 3 . The mass of block B is-
 Am/2Bm/3C2m/3Dm/√3
Am/2Bm/3C2m/3Dm/√3Two blocks of mass 2m and m slide down the slope AB having same friction coefficient Then:
 Athe heavier mass reaches the bottom in a shorter timeBboth the masses have the same kinetic energy on arriving at BCthe heavier mass has twice the momentum than that of the other when reaching BDthe lighter mass reaches the bottom in a shorter time
Athe heavier mass reaches the bottom in a shorter timeBboth the masses have the same kinetic energy on arriving at BCthe heavier mass has twice the momentum than that of the other when reaching BDthe lighter mass reaches the bottom in a shorter time
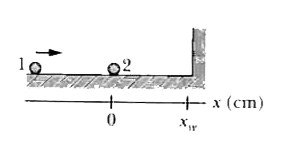
In Fig., particle 1 of mass m1 = 0.30 kg slides rightward along an x axis on a frictionless floor with a speed of 2.0 m/s. When it a one-dimensional elastic collision with stationary particle 2 of mass m2 = 0.40 kg. When particle 2 then reaches a wall at xw = 70 cm, it bounces from the wall with no loss of speed. At what position on the x axis does particle 2 then collide with particle 1 ?
View SolutionA block of mass m=3kg slides on a rough inclined plane of cofficient of friction 0.2 Find the resultant force offered by the plane on the block

View SolutionIn Fig. a stationary block explodes into two pieces L and R that slide across a frictionless floor and then into regions with friction, where they stop. Piece L. with a mass of 2.0 kg, encounters a coefficient of kinetic friction μL = 0.35 and slides to a stop in distance dL =0.15 m. Piece R encounters a coefficient of kinetic friction μR=0.50 and slides to a stop in distance dR =0.30 m. What was the mass of the block?

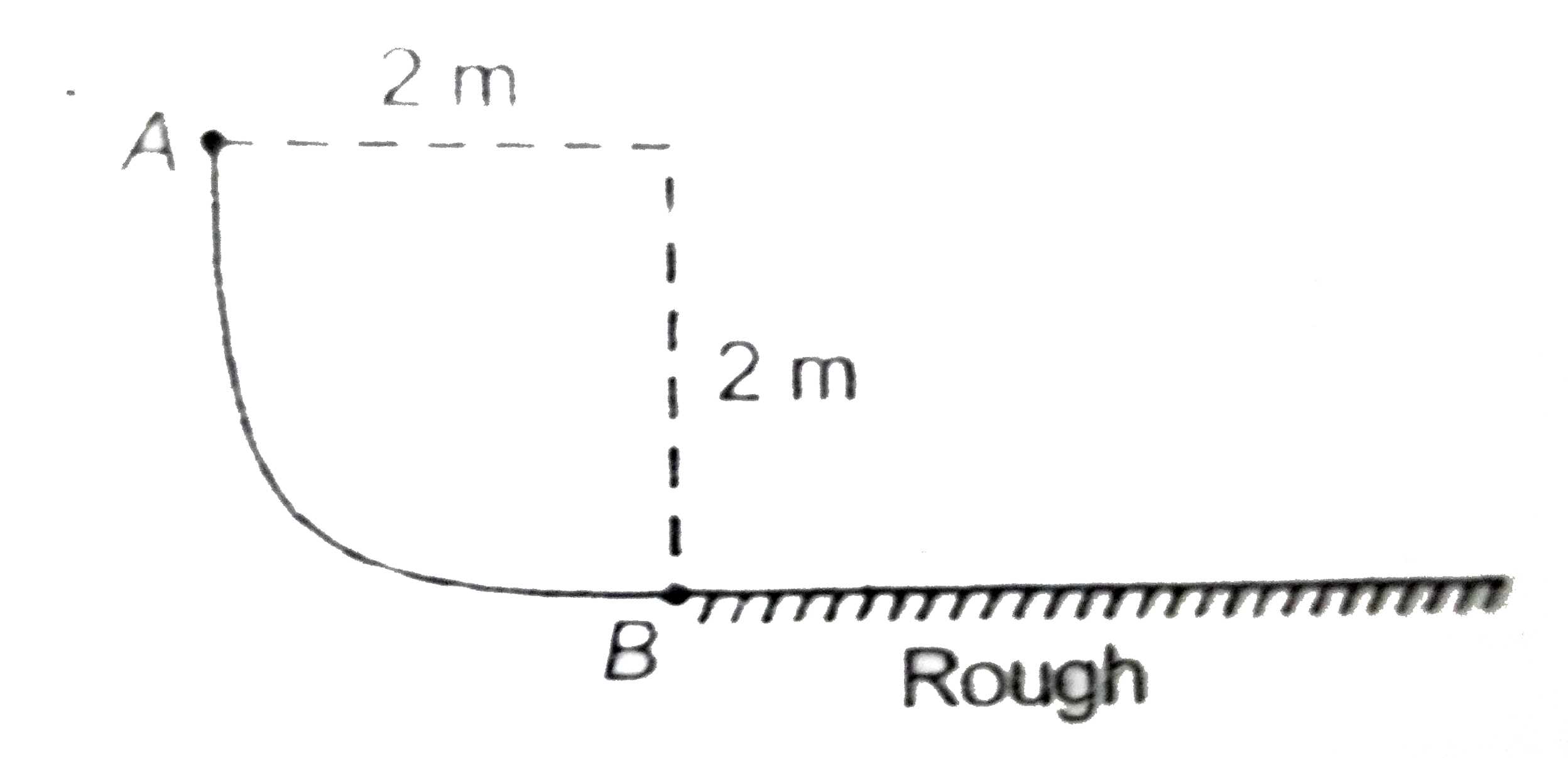
View SolutionA block is released at A and slides on smooth surface in shape of quarter circel. The horizontal part is rough if the block comes to rest 1.0 m away from B, then what is the coefficient of kinetic friction?
View SolutionA block of mass 50 kg slides over a horizontal distance of 1m. If the coefficient of friction between their surface is 0.2, then work done against friction is (take g=9.8m/s2) :
View Solution
