A bug is crawling with constant speed v, along the spoke of a bicycle wheel, of radius a while the bicycle moves down the road with constant speed v. Find the accelerations of the bug as observed by a man standing beside the road, along the perpendicular to the spoke of the wheel.
The correct Answer is:(a) ar=RV2a2; (b) aθ=2vVa
To solve the problem, we need to analyze the motion of the bug as it crawls along the spoke of the bicycle wheel while the bicycle moves down the road. We will determine the acceleration of the bug as observed by a man standing beside the road.
1. Understanding the Motion:
- The bug is crawling along the spoke of the wheel with a constant speed v.
- The bicycle is moving down the road with a constant speed v.
- The radius of the bicycle wheel is a.
2. Identifying the Components of Motion:
- The bug's motion can be broken down into two components:
- Radial motion (along the spoke of the wheel).
- Tangential motion (due to the rotation of the wheel).
3. Calculating Radial Acceleration:
- The radial acceleration ar of the bug can be calculated using the formula for radial acceleration:
ar=v2a
- Here, v is the speed of the bug along the spoke, and a is the radius of the wheel.
4. Calculating Tangential Acceleration:
- The bug also experiences tangential acceleration due to the movement of the bicycle. Since the bicycle is moving at a constant speed v, the tangential acceleration at can be expressed as:
at=2v⋅va=2v2a
- This accounts for the effect of the bicycle's speed on the observed motion of the bug.
5. Total Acceleration:
- The total acceleration a of the bug as observed by the man standing beside the road is the vector sum of the radial and tangential accelerations. However, since we are interested in the component of acceleration perpendicular to the spoke, we can focus on the tangential component:
a_{\perpendicular} = a_t = \frac{2v^2}{a}
Final Answer:
The acceleration of the bug as observed by a man standing beside the road, along the perpendicular to the spoke of the wheel, is given by:
a_{\perpendicular} = \frac{2v^2}{a}
- The bug is crawling along the spoke of the wheel with a constant speed v.
- The bicycle is moving down the road with a constant speed v.
- The radius of the bicycle wheel is a.
- The bug's motion can be broken down into two components:
- Radial motion (along the spoke of the wheel).
- Tangential motion (due to the rotation of the wheel).
- The radial acceleration ar of the bug can be calculated using the formula for radial acceleration:
ar=v2a
- Here, v is the speed of the bug along the spoke, and a is the radius of the wheel.
- The bug also experiences tangential acceleration due to the movement of the bicycle. Since the bicycle is moving at a constant speed v, the tangential acceleration at can be expressed as:
at=2v⋅va=2v2a
- This accounts for the effect of the bicycle's speed on the observed motion of the bug.
- The total acceleration a of the bug as observed by the man standing beside the road is the vector sum of the radial and tangential accelerations. However, since we are interested in the component of acceleration perpendicular to the spoke, we can focus on the tangential component:
a_{\perpendicular} = a_t = \frac{2v^2}{a}
The acceleration of the bug as observed by a man standing beside the road, along the perpendicular to the spoke of the wheel, is given by:
a_{\perpendicular} = \frac{2v^2}{a}
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - PRACTICE QUESTIONS(SINGLE CORRECT CHOICE TYPE)
40 Videos
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - PRACTICE QUESTIONS(MORE THAN ONE CORRECT CHOICE TYPE)
6 Videos
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - CHECK POINTS
6 Videos
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)
3 Videos
- CURRENT AND RESISTANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CURRENT AND RESISTANCEEXERCISE - Practice Questions (Integer Type)
3 Videos
Similar Questions
The speed (v) of a particle moving in a circle of radius R varies with distance s as v=ks where k is a positive constant.Calculate the total acceleration of the particle
View SolutionA particle moves along on a road with constant speed at all points as shown in figure. The normal reaction of the road on the particle is :
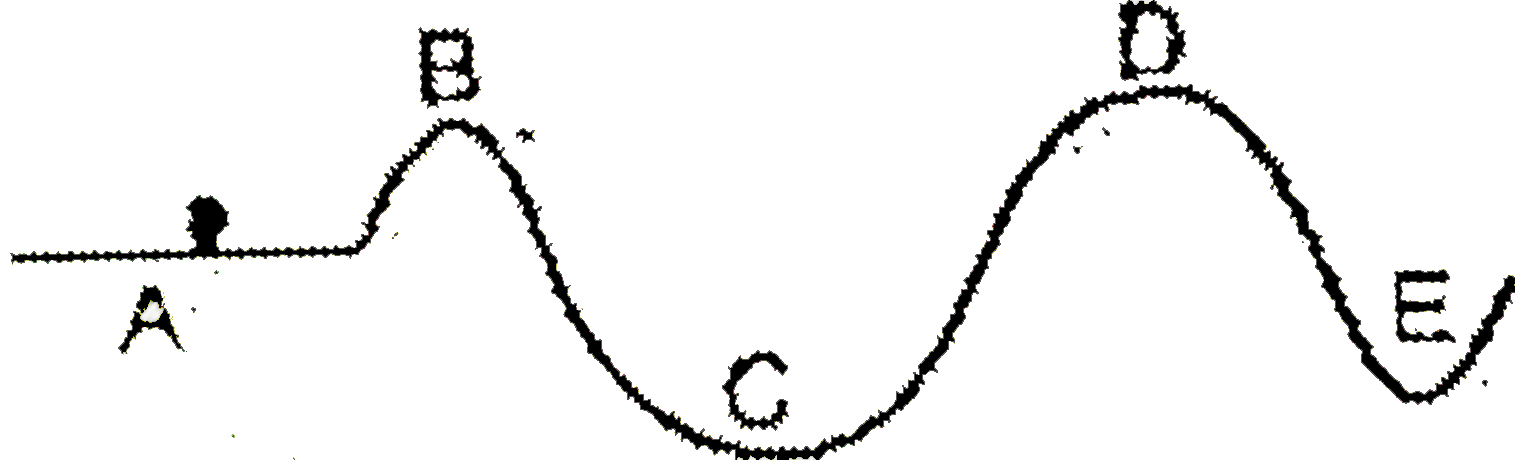
View Solution
Knowledge Check
A bicycle is moving on a straight road at a constant speed. The wheels of the cycle exhibit :
ACircular, translational and periodic motionBCircular and translational motionCTranslational and periodic motionDCircular and periodic motionA car is moving along a straight level road with constant speed. Then
Athe work done on the car is infiniteBthe work done on the car is zeroCthe work done on the car is a measure of the gravitational potential energyDthe work done on the car cannot be foundA car is moving along a straight level road with constant speed. Then
Athe work done on the car is a.measure of.its gravitational P.E.Bthe work one on the car is zero.Cthe work done on the car cannot. be foundDthe work done on the'car is infinite.
A particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
View SolutionAn electron moves with a constant speed v along a circle of radius r. Its magnetic moment will be (e is the electron's charge)
View Solution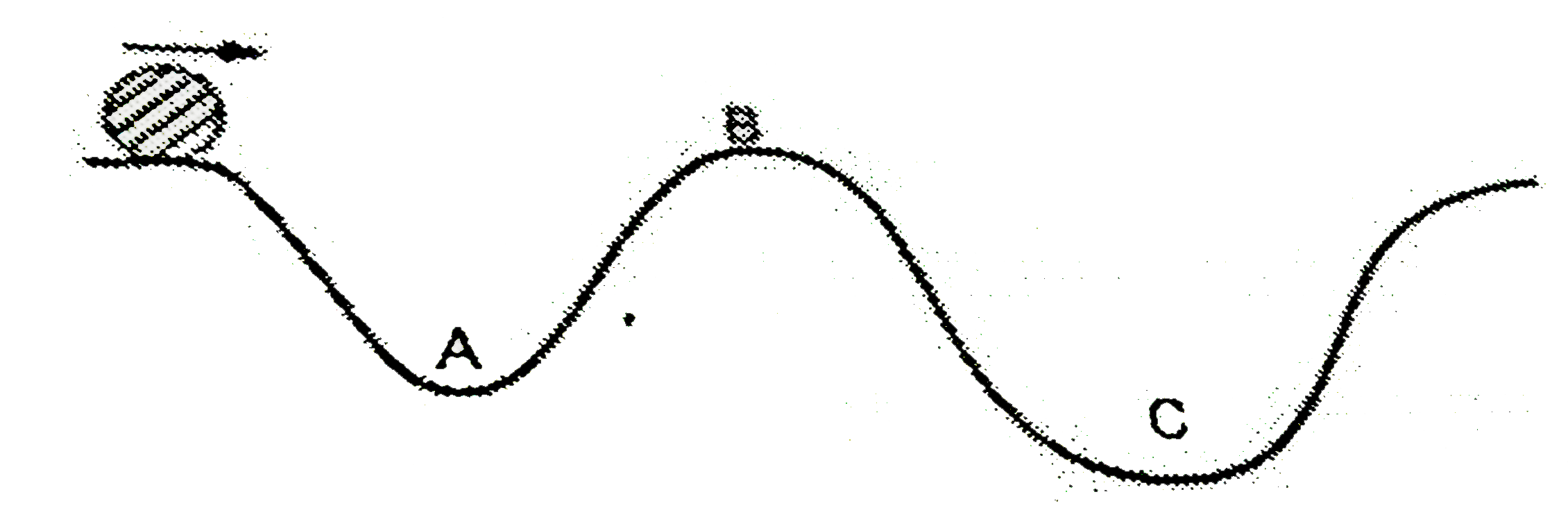
A body moves along an uneven horizontal road surface with constant speed at all points. The normal reaction of the road on the body is
View SolutionAn electron moves with a constant speed v along a circle of radius r. Its magnetic moment will be (e = eletronic charge)
View SolutionConsider a wheel of a bicycle rolling on a level road at a liner speed v0 figure.

View Solution
