A layer of glycerine of thickness 1 mm is present between a large surface and small surface of area 0.1m2. With what force the small surface is to be pulled, so that it can move with a velocity of 1 m/s ?
(coefficient of viscosity=0.07g−m−1s−1)
70N
7N
700 N
0.70N
The correct Answer is:B
To solve the problem of determining the force required to pull the small surface through a layer of glycerine, we can use the formula for viscous force. The viscous force (F) can be calculated using the equation:
F=η⋅A⋅dvdx
Where:
- η is the coefficient of viscosity,
- A is the area of the surface,
- dvdx is the velocity gradient.
Step 1: Identify the given values
- Coefficient of viscosity (η) = 0.07 g/m·s = 0.07 × 10^-3 kg/m·s (since 1 g = 10^-3 kg)
- Area (A) = 0.1 m²
- Velocity (v) = 1 m/s
- Thickness of glycerine layer (d) = 1 mm = 1 × 10^-3 m
Step 2: Calculate the velocity gradient (dvdx)
The velocity gradient is defined as the change in velocity per unit distance. Here, since the small surface moves with a constant velocity and the thickness of the glycerine layer is the distance over which this velocity change occurs, we can express the velocity gradient as:
dvdx=vd
Substituting the known values:
dvdx=1m/s1×10−3m=1000s−1
Step 3: Substitute the values into the viscous force equation
Now we can substitute the values into the viscous force equation:
F=η⋅A⋅dvdx
Substituting the values we have:
F=(0.07×10−3kg/m⋅s)⋅(0.1m2)⋅(1000s−1)
Step 4: Calculate the force
Now, we perform the calculation:
F=0.07×10−3⋅0.1⋅1000
F=0.07×0.1×1
F=0.007N
Final Answer
The force required to pull the small surface is 0.007 N.
---
- η is the coefficient of viscosity,
- A is the area of the surface,
- dvdx is the velocity gradient.
- Coefficient of viscosity (η) = 0.07 g/m·s = 0.07 × 10^-3 kg/m·s (since 1 g = 10^-3 kg)
- Area (A) = 0.1 m²
- Velocity (v) = 1 m/s
- Thickness of glycerine layer (d) = 1 mm = 1 × 10^-3 m
The velocity gradient is defined as the change in velocity per unit distance. Here, since the small surface moves with a constant velocity and the thickness of the glycerine layer is the distance over which this velocity change occurs, we can express the velocity gradient as:
Now we can substitute the values into the viscous force equation:
Now, we perform the calculation:
The force required to pull the small surface is 0.007 N.
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Properties of Matter & Fluid Mechanics)(Hydrostatics)
20 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Properties of Matter & Fluid Mechanics)(Surface Tension)
26 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Properties of Matter & Fluid Mechanics)(Elasticity)
20 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Video
Similar Questions
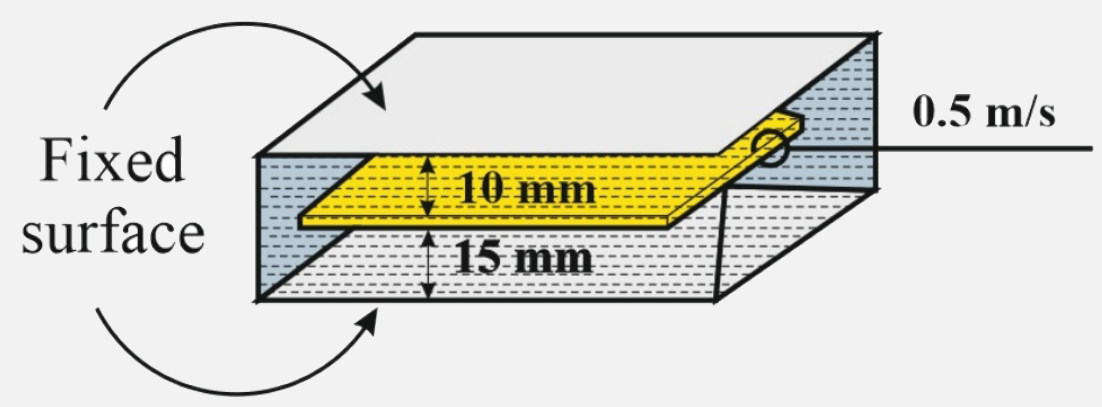
Glycerine is filled is 25mm wide space between two large plane horizontal surfaces. Calculate the force required to drag a very thin plate 0.75m2 in area between the surface at a constant speed of 0.5m/s if it is at a distance of 10mm from of the surfaces in horizontal position? Take coefficient of viscosity η=0.5Ns/m2. Fill the value of X where X= force required to drag/6.25

View SolutionGlycerine is filled in 25 mm wide space between two large plane horizontal surfaces. A thin plate of area 0.75m2 at a distance of 10 mm from one of the surfaces is in a horizontal position be the plates inside the glycerine. It is dragged horizontally at a constant speed of 0.5ms2. Take coefficient of viscosity η= 0.5 Ns m−2. What is the force required to drag the plate at a constant speed (in newton) ?
View Solution
Knowledge Check
There is a 1 mm thick layer of oil between a flat plate of area 10−2m2 and a big plate. How much force is required to move the plate with a velocity of 1.5cm/s. The coefficient of viscosity of oil is 1 poise
A1.5×10−3NB1.3×10−5NC1.5×10−2ND1.5×102NA metal plate of area 500cm92) is kept on a horizontal surface with a layer of oil of thickness 0.5 mm between them. The horizontal force required to drag the plate with a velocity of 2 cm/s is
(coefficient of viscosity =0.9 kg/ms)A180 NB18 NC0.018 ND1.8NThe surface tension of water is 0.07 N/m . Find the weight of water supported by surface tension in a capillary tube with a radius of 0.1 mm.
A11μNB22μNC44μND88mμN
The force of 2000 dyne is required to move a flat glass plate of surface area 10cm2 with a velocity of 1 cm/s over a surface of glycerine 1 mm thick. The coefficient of viscosity of glycerine is
View Solution
A space 2.5cm wide between two large plane surfaces is filled with oil. Force required to drag a very thin plate of area 0.5m2 just midway the surfaces at a speed of 0.5msec is 1N. The coefficient of viscosity in kg−sm2 is:
View SolutionA disc of mass 2 kg is rolling on a horizontal surface without slipping with a velocity of 0.1 m/s. What is its rotational kinetic energy?
View SolutionAll surfaces assumed to be frictionless calculate the horizontal force F that must be applied so that m1 and m2 do not move relative to m3 is :–

View SolutionA metal plate of area 20 cm2, is separated from a large plate by a layer of glycerine I mm thick. The coefficient of Viscosity of the glycerine is 20 poise. What is the honz?ntal force required to keep the plate moving with a velocity of 2 cm/s?
[poise=10−1N−s/m2]
View Solution
