Young's modulus of brass and steel are 10×1010N/m2 and 2×1011N/m2, respectively. A brass wire and a steel wire of the same length are extended by 1mm under the same force. The radii of the brass and steel wires are RB and RS respectively. Then
RS=√2RB
RS=RB√2
RS=4RB
RS=RB4
The correct Answer is:B
Step by step video, text & image solution for Young's modulus of brass and steel are 10 xx 10^(10) N//m^(2) and 2 xx 10^(11) N//m^(2), respectively. A brass wire and a steel wire of the same length are extended by 1 mm under the same force. The radii of the brass and steel wires are R_(B) and R_(S) respectively. Then by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Properties of Matter & Fluid Mechanics)(Fluid Dynamics + Viscosity)20videos
RACE
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Properties of Matter & Fluid Mechanics)(Hydrostatics)20videos
RACE
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (GRAVITATION)25videos
RACE
- BOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III28videos
NEWTONS LAWS OF MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example1videos
SIMPLE HARMONIC MOTION
Similar Questions
Young's modulus of brass and steel are 10×1010N/m and 2×1011N/m2, respectively. A brass wire and a steel wire of the same length are extended by 1mm under the same force. The radii of the brass and steel wires are RB and RS. respectively. Then
View SolutionThe Young's modulus of brass and steel are 10×1010Nm−2and20×1010Nm−2 respectively. A brass wire and steel wire of the same length are extended by 1 mm under the same force. If the radii of the brass and steel wires are RBandRS respectively, then
View SolutionThe young 's modulus of brass and steel are 1.0×1011Nm−2 and 2.0×1011N/m2. Respectively . A brass wire and steel wire of the same length extend by 1 mm, each under the same forece . It radii of brass and steel wires are RB and RS respectively, them
View SolutionThe Young's modulus of brass and steel are respectively 1.0×1011Nm−2 and 2.0×1011Nm−2. A brass wire and a steel wire of the same length are extended by 1 mm each under the same force. If radii of brass and steel wires are RB and Rs respectively, then
View SolutionThe Young's modulus of brass and steel are respectively 1.0×1011N/m2 and 2.0×1011N/m2 . A brass wire and steel wire of the same length are extended by 1mm each under the same force. If radii of brass and steel wires are RB and RS respectively,. then
View SolutionThe Young's modulii of brass ans steel are in the ratio of 1:2. A brass wire and a steel wire of the same length are extended by the same amount under the same deforming force. If rB and rS are the radii of brass and steel wires respectively, then
View SolutionYoung 's modulus of steel is 2.0×1011Nm/(2). Express it is dynecm2.
View SolutionYoung's modulus for a steel wire is 2 × 1011 Pa and its elastic limit is 2.5 × 108Pa. By how much can a steel wire 3 m long and 2 mm in diameter be stretched before the elastic limit is exceeded ?
View SolutionA block of weight 100 N is suspended by copper and steel wires of same cross sectional area 0.5cm2 and, length √3 m and 1m, respectively. Their other ends are fixed on a ceiling as shown in figure. The angles subtended by copper and steel wires with ceiling are 30∘and60∘, respectively. If elongation in copper wire is (ΔlC) and elongation in steel wire is (Δls), then the ratio ΔlCΔls is -
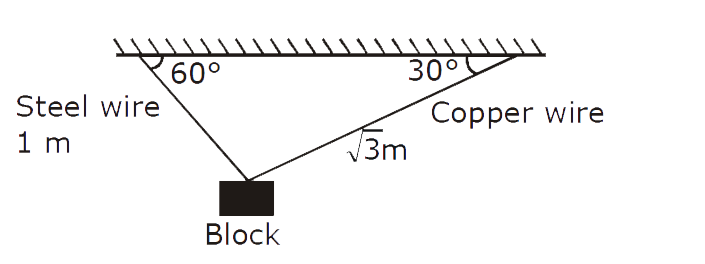
[Young's modulus for copper and steel are 1×1011N/m2and2×1011N/m2, respectively]View SolutionYoung's modulus for steel is 2×1010N/m2. If the interatomic distance for steel is 3 Å, then the interatomic force constant for steel will be
View Solution


