An observer is travelling in east with a velocity of 2 m/s and observes that wind is blowing in north with a velocity of 2m/s. If observer doubles his velocity then find out the velocity of wind appears to observer ?
The correct Answer is:2√2m/s N-W
To solve the problem, we need to find the apparent velocity of the wind as observed by an observer who doubles his velocity. We will break this down step by step.
Step 1: Understand the Initial Conditions
- The observer is moving east with a velocity of vo=2m/s.
- The wind is blowing north with a velocity of vw=2m/s.
Step 2: Represent the Velocities as Vectors
- The observer's velocity can be represented as:
→vo=2^im/s
- The wind's velocity can be represented as:
→vw=2^jm/s
Step 3: Calculate the Relative Velocity of Wind with Respect to Observer
- The apparent velocity of wind with respect to the observer is given by:
→vw/o=→vw−→vo
- Substituting the values:
→vw/o=(2^j)−(2^i)=−2^i+2^j
Step 4: Find the Magnitude and Direction of the Relative Velocity
- The magnitude of the relative velocity can be calculated as:
|→vw/o|=√(−2)2+(2)2=√4+4=√8=2√2m/s
- The direction can be determined using the arctangent function:
θ=tan−1(2−2)=tan−1(−1)
This indicates that the direction is towards the northwest.
Step 5: Double the Observer's Velocity
- If the observer doubles his velocity, then:
v′o=2×2=4m/s
- The new velocity vector of the observer becomes:
→v′o=4^im/s
Step 6: Calculate the New Apparent Velocity of Wind
- The new apparent velocity of wind with respect to the observer is:
→vw/o′=→vw−→v′o
- Substituting the values:
→vw/o′=(2^j)−(4^i)=−4^i+2^j
Step 7: Find the Magnitude and Direction of the New Relative Velocity
- The magnitude of the new relative velocity can be calculated as:
|→vw/o′|=√(−4)2+(2)2=√16+4=√20=2√5m/s
- The direction can be determined using the arctangent function:
θ′=tan−1(2−4)=tan−1(−12)
This indicates that the direction is towards the northwest.
Final Answer
The velocity of the wind as observed by the observer after doubling his velocity is 2√5m/s towards the northwest.
---
- The observer is moving east with a velocity of vo=2m/s.
- The wind is blowing north with a velocity of vw=2m/s.
- The observer's velocity can be represented as:
→vo=2^im/s
- The wind's velocity can be represented as:
→vw=2^jm/s
- The apparent velocity of wind with respect to the observer is given by:
→vw/o=→vw−→vo
- Substituting the values:
→vw/o=(2^j)−(2^i)=−2^i+2^j
- The magnitude of the relative velocity can be calculated as:
|→vw/o|=√(−2)2+(2)2=√4+4=√8=2√2m/s
- The direction can be determined using the arctangent function:
θ=tan−1(2−2)=tan−1(−1)
This indicates that the direction is towards the northwest.
- If the observer doubles his velocity, then:
v′o=2×2=4m/s
- The new velocity vector of the observer becomes:
→v′o=4^im/s
- The new apparent velocity of wind with respect to the observer is:
→vw/o′=→vw−→v′o
- Substituting the values:
→vw/o′=(2^j)−(4^i)=−4^i+2^j
- The magnitude of the new relative velocity can be calculated as:
|→vw/o′|=√(−4)2+(2)2=√16+4=√20=2√5m/s
- The direction can be determined using the arctangent function:
θ′=tan−1(2−4)=tan−1(−12)
This indicates that the direction is towards the northwest.
The velocity of the wind as observed by the observer after doubling his velocity is 2√5m/s towards the northwest.
Topper's Solved these Questions
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (NEWTONS LAWS OF MOTION)
Explore 44 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (FRICTION)
Explore 11 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Units, Dimensions & Measurements)
Explore 33 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
Similar Questions
An observer is travelling in west with velocity of 5 km/h and observes that wind is blowing in north with the velocity of 5√3 km/h. Find out the actual velocity of wind.
View SolutionThe wind is blowing in south with velocity of 4 km/h and abserver is travelling with velocity of 4√3 km/h in east. Find out the velocity of wind appeared to observer.
View Solution
Knowledge Check
A car is going east wards with a velocity of 8m/s. To the passengers in the car, a train appears to be moving north wards with a velocity of 15 m/s. What is the actual velocity of the train:
A7 m/sB17 m/sC23 m/sDNone of theseAn observer A is at rest in gournd frame, observer B is moving with constant another observer C is moving with constant velocity of 1m/s.
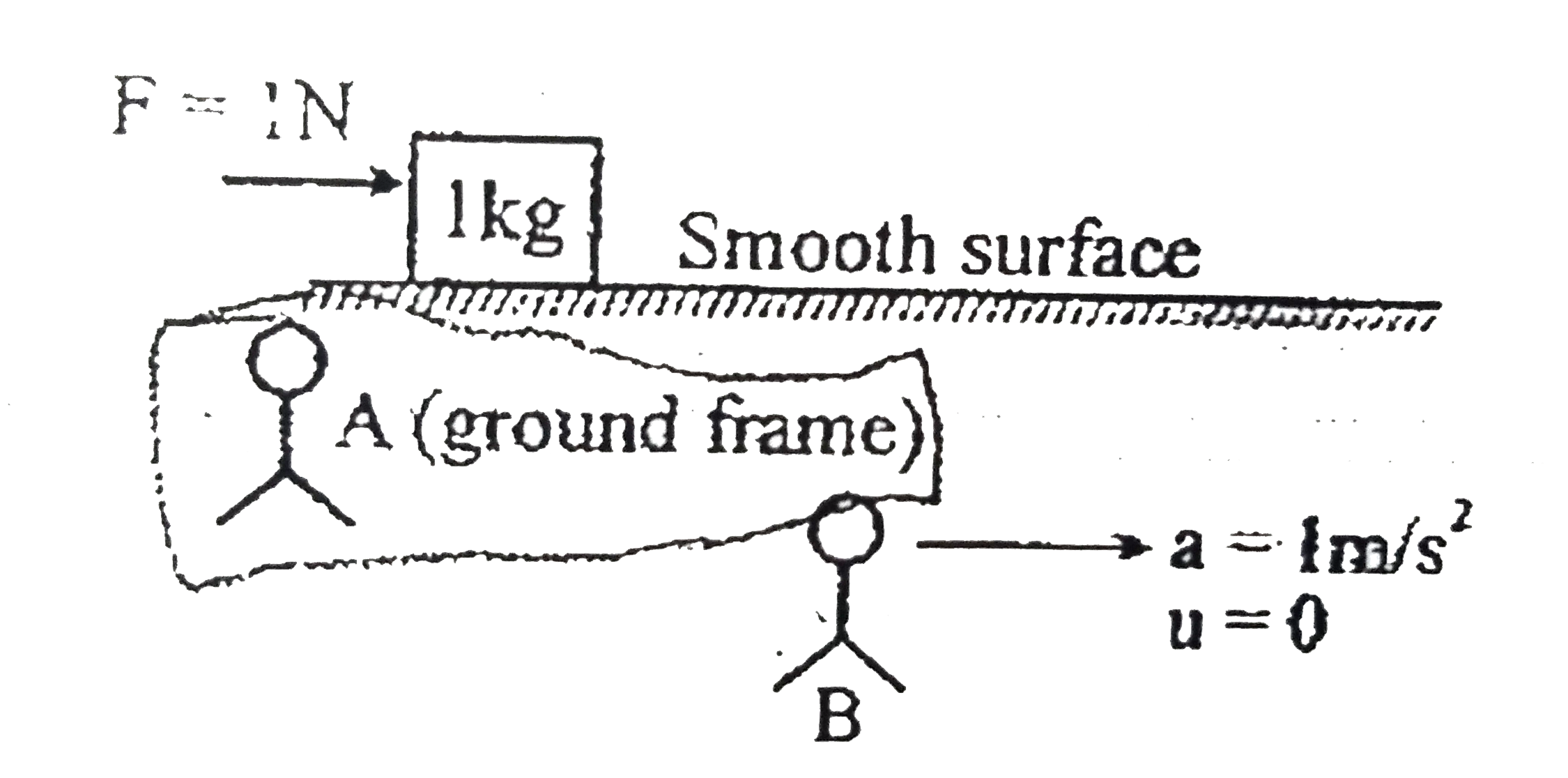 Awork done by all forces (both real and pseudo) in 1 sec in frame of A is 0.5JBwork done by all forces (both real and pseudo) in 1 sec in frame of B is 0JCwork done by all force (both real and pseudo) in 1 sec in frame of C is -0.5JDchange in K.E. in frame of B is zero
Awork done by all forces (both real and pseudo) in 1 sec in frame of A is 0.5JBwork done by all forces (both real and pseudo) in 1 sec in frame of B is 0JCwork done by all force (both real and pseudo) in 1 sec in frame of C is -0.5JDchange in K.E. in frame of B is zeroA motor car A is travelling with a velocity of 20m/s in the north-west direction and another motor car B is travelling with a velocity of 15m/s in the north-east directions.The magnitude of relative velocity of B with respect to A is.
A25m/sB15m/sC20m/sD35m/s
A person moves due east at speed 6m/s and feels the wind is blowing to south at speed 6 m/s.
(a) Find actual velocity of wind blow.
(b) If person doubles his velocity then find the relative velocity of wind blow w.r.t. man.
View SolutionRain is falling vertically downwards with a velocity of 2m//s. A person is runing to the North with a velocity of 2√3m/s. Find out the velocity and direction of rain as appeared to the person.
View SolutionA bird is fying due east with a velocity of 4ms−1. The starts to blow with a velocity of 3ms−1 due north. What is the magnituide of relative velocity of bird w.r.t. wind ? Find out its direction also.
View SolutionA boat is moving towards south with veloctity 3m/s with respect to still water and river is flowing towards east with velocity 3m/s and the wind is blowing towards south-east with velocoity 3√2m/s. The direction of the flag blown over by the wind, hoisted on the boat is :
View SolutionOut of the two cars A and B car A is moving towards east with velocity of 10 m/s whereas B is moving towards north with a velocity 20 m/s, then velocity of A w.r.t B is ( nearly )
View Solution

