Which of the following relation cannot be deduced using dimensional analysis ? [the symbols have their usual meanings]
y=Asin(ωt+kx)
v=u+at
k=12mv2
All of these
The correct Answer is:D
To solve the question regarding which relation cannot be deduced using dimensional analysis, we will follow a step-by-step approach.
Step 1: Understand Dimensional Analysis
Dimensional analysis is a method used in physics to analyze the dimensions of physical quantities. It helps in checking the consistency of equations and deriving relationships between different physical quantities. However, it has limitations.
Step 2: Identify the Limitations
The key limitation of dimensional analysis is that it can only be used to deduce relationships involving products of quantities raised to powers (i.e., power functions). It cannot be used to deduce relationships involving sums or differences of quantities.
Step 3: Analyze the Options
Now, we need to analyze the options provided in the question. The options typically involve relationships between physical quantities, such as:
1. Equating dimensions of different quantities.
2. Relationships involving sums (e.g., A+B).
3. Relationships involving products (e.g., A×B).
4. Specific equations like kinetic energy K=12mv2.
Step 4: Evaluate Each Option
- Option 1: Equating dimensions of two quantities can be done using dimensional analysis.
- Option 2: If the relation involves a sum (e.g., A+B), dimensional analysis cannot be used to derive this directly.
- Option 3: Relationships involving products can be analyzed using dimensional analysis.
- Option 4: The equation for kinetic energy K=12mv2 involves a constant (1/2) which cannot be derived from dimensional analysis alone.
Step 5: Conclusion
Since dimensional analysis cannot deduce relationships involving sums or constants, the option that cannot be deduced using dimensional analysis is the one involving sums or specific constants in equations.
Final Answer
Thus, the relation that cannot be deduced using dimensional analysis is all of these, as they all involve either sums or constants.
---
Dimensional analysis is a method used in physics to analyze the dimensions of physical quantities. It helps in checking the consistency of equations and deriving relationships between different physical quantities. However, it has limitations.
The key limitation of dimensional analysis is that it can only be used to deduce relationships involving products of quantities raised to powers (i.e., power functions). It cannot be used to deduce relationships involving sums or differences of quantities.
Now, we need to analyze the options provided in the question. The options typically involve relationships between physical quantities, such as:
1. Equating dimensions of different quantities.
2. Relationships involving sums (e.g., A+B).
3. Relationships involving products (e.g., A×B).
4. Specific equations like kinetic energy K=12mv2.
- Option 1: Equating dimensions of two quantities can be done using dimensional analysis.
- Option 2: If the relation involves a sum (e.g., A+B), dimensional analysis cannot be used to derive this directly.
- Option 3: Relationships involving products can be analyzed using dimensional analysis.
- Option 4: The equation for kinetic energy K=12mv2 involves a constant (1/2) which cannot be derived from dimensional analysis alone.
Since dimensional analysis cannot deduce relationships involving sums or constants, the option that cannot be deduced using dimensional analysis is the one involving sums or specific constants in equations.
Thus, the relation that cannot be deduced using dimensional analysis is all of these, as they all involve either sums or constants.
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (KINEMATICS)
59 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (NEWTONS LAWS OF MOTION)
44 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (VECTORS)
57 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Video
Similar Questions
Knowledge Check
Bohr magnetonis given by (symbols have their usual meanings)
A4πmeeh2B4πmeehCeh24πmeDeh4πmeWhich one of the following is equation of the modulus of rigidity?
(Where the symbols have their usual meanings)Aη=FLAlBη=VdpdvCη=FhAxDη=d/Dl/LThe correct combination is (symbols have their usual meanings)
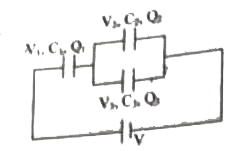 AQ1=Q2=Q3andV1=V2=V3=VBQ1=Q2+Q3andV=V1+V2+V3CQ1=Q2+Q3andV=V1+V2DQ2=Q3andV2=V3
AQ1=Q2=Q3andV1=V2=V3=VBQ1=Q2+Q3andV=V1+V2+V3CQ1=Q2+Q3andV=V1+V2DQ2=Q3andV2=V3
Which of the following is correct expression for the stopping distance of a vechicle? (symbols have their usual meaning)
View SolutionWhich of the following relations does not give the equation of an adiabatic process, where tems have their usual meaning ?
View SolutionMechanically work done is equal to (symbols have their usual meanings)
View SolutionMechanically work done is equal to (symbols have their usual meanings)
View SolutionWhich of the following can be used to express energy ?The symbols used have their usual meanings for the units of physical quantities.
(i) Wh (ii) VC
(iii) AVs2
(iv) A2Ωs
View Solution
