If →P=−−→KQ (Here K is constant) them :-
→P∣∣→Q
→P∣∣→Q
→P⊥→Q
Both (1) and (2)
The correct Answer is:D
To solve the problem where →P=K→Q (with K being a constant), we can follow these steps:
1. Understanding the Equation:
The equation →P=K→Q indicates that vector →P is a scalar multiple of vector →Q. Here, K is a constant.
2. Analyzing the Implication:
Since →P is equal to K times →Q, it implies that the direction of →P is the same as that of →Q if K is positive. If K is negative, →P will be in the opposite direction of →Q.
3. Magnitude Consideration:
The magnitudes of the vectors are related by the equation:
|→P|=|K||→Q|
This means that the magnitude of →P will be proportional to the magnitude of →Q by the factor of |K|.
4. Conclusion about Parallelism:
Since →P is a scalar multiple of →Q, we conclude that →P and →Q are parallel vectors. This holds true regardless of whether K is positive or negative.
5. Final Answer:
Therefore, the correct conclusion is that →P is parallel to →Q.
The equation →P=K→Q indicates that vector →P is a scalar multiple of vector →Q. Here, K is a constant.
Since →P is equal to K times →Q, it implies that the direction of →P is the same as that of →Q if K is positive. If K is negative, →P will be in the opposite direction of →Q.
The magnitudes of the vectors are related by the equation:
|→P|=|K||→Q|
This means that the magnitude of →P will be proportional to the magnitude of →Q by the factor of |K|.
Since →P is a scalar multiple of →Q, we conclude that →P and →Q are parallel vectors. This holds true regardless of whether K is positive or negative.
Therefore, the correct conclusion is that →P is parallel to →Q.
Topper's Solved these Questions
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Units, Dimensions & Measurements)
Explore 33 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (KINEMATICS)
Explore 59 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Co-ordinate & Algebra)
Explore 39 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
Similar Questions
Knowledge Check
→p,→q,→ be vectors such that →q.→r=0 and →p.→q≠0. Let α is real constant such that →x.→p=α,→x×→q=→r, then →x−λ1→q=λ2(→p×→r) where
Aλ1=α→p.→qBλ2=1→p.→qCλ2=1→r.→qDλ1=α→r.→qThree vectors →P,→Q and →R are shown in the figure. Let S be any point on the vector →R. The distance between the points P and S is b∣∣→R∣∣. The general relation among vectors→P,→Q and →S is:
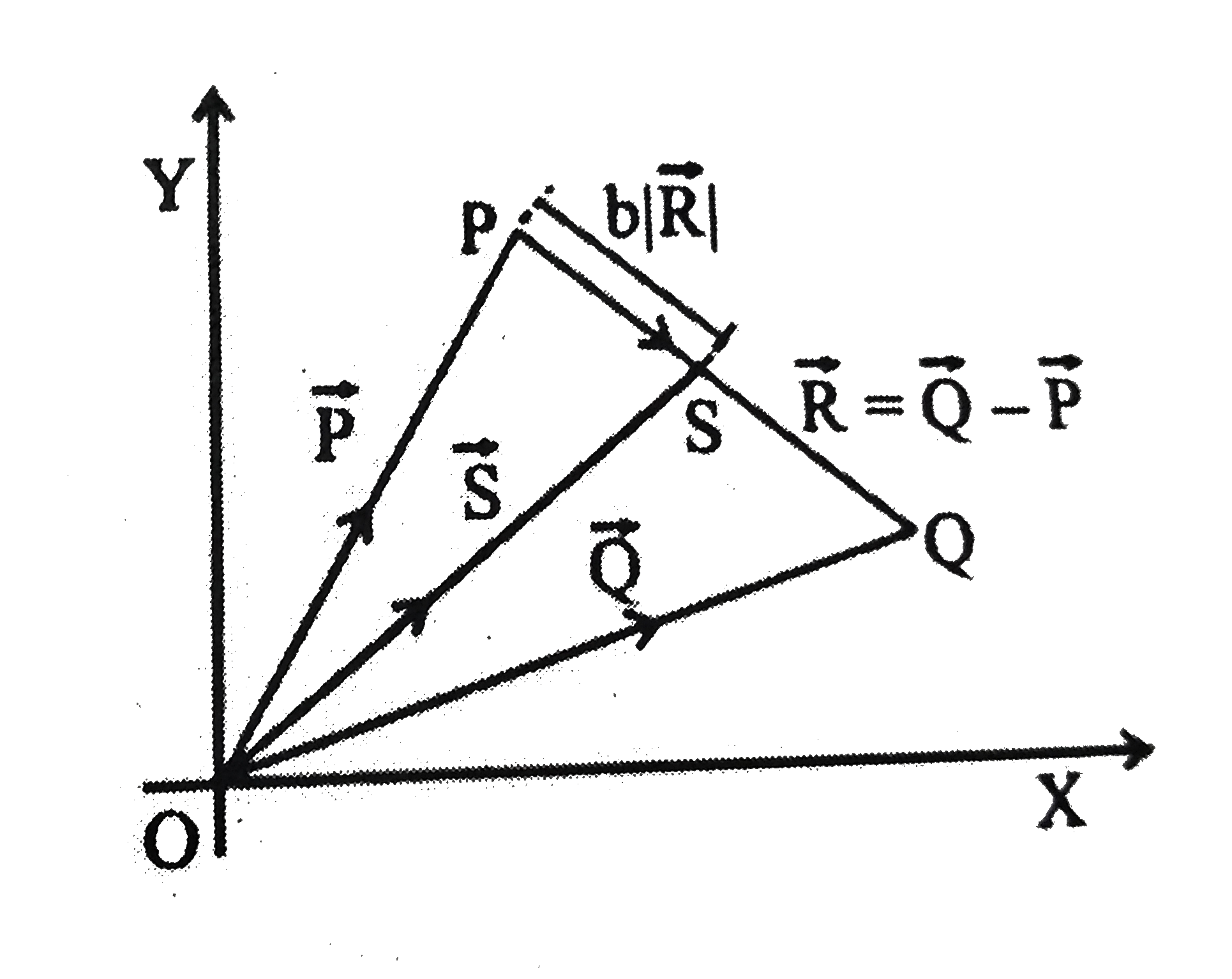 A→S=(1−b)→P+b2→QB→S=(b−1)→P+b→QC→S=(1−b)→P+b→QD→S=(1−b2)→P+b→Q
A→S=(1−b)→P+b2→QB→S=(b−1)→P+b→QC→S=(1−b)→P+b→QD→S=(1−b2)→P+b→QAccording to Charle's law (here k is constant of proportionality)
A(dV/dT)P=KB(dV/dT)P=−KC(dV/dT)P=−K/TDNone of these
Two foreces →Pand→Q are acting at a point . If →P is reversed, the new resultant becomes between magnitudes of P and Q is given by P=KQ. Find k.
View SolutionIf two vectors →a,→b are such that ∣∣→a.→b∣∣=∣∣→a×→b∣∣ then angle between them is
View Solutionif →Pa+→Q=→0 , then which of the following is necessarily true ?
View SolutionGiven that P=Q=R. If →P+→Q=→R then the angle between →P&→R is θ1. If →P+→Q+→R=→0 then the angle between →P&→R is θ2. What is the relation between θ1andθ2 ?
View SolutionThree vectors →a,→band→c are of the same length and the angle between any two of them is the same. If →a=ˆi+ˆjand→b=ˆj+ˆk, then →c is
View Solution

