An ideal gas is subjected to a thermodynamic process where P is in Pa and V is in . What is the slope of the P-V curve with volume plotted against x-axis at V=1 ?
-1
-3.5
-2.5
None of these
The correct Answer is:A
To find the slope of the P-V curve for the given thermodynamic process PV2/5=0.40, we can follow these steps:
Step 1: Rearranging the equation
We start with the equation:
PV2/5=0.40
To express P in terms of V, we rearrange the equation:
P=0.40V2/5
Step 2: Differentiating P with respect to V
Next, we need to find the slope of the curve, which is given by dPdV. We will differentiate P with respect to V:
P=0.40⋅V−2/5
Using the power rule of differentiation, where ddx(xn)=nxn−1, we differentiate:
dPdV=0.40⋅(−25)V−2/5−1
This simplifies to:
dPdV=−0.805V−7/5=−0.16V7/5
Step 3: Evaluating the derivative at V=1m3
Now, we need to evaluate this derivative at V=1m3:
dPdV∣∣∣V=1=−0.16(1)7/5=−0.16
Step 4: Interpreting the result
The slope of the P-V curve at V=1m3 is:
dPdV=−0.16Pa/m3
Conclusion
Thus, the slope of the P-V curve at V=1m3 is −0.16 Pa/m³.
We start with the equation:
PV2/5=0.40
To express P in terms of V, we rearrange the equation:
P=0.40V2/5
Next, we need to find the slope of the curve, which is given by dPdV. We will differentiate P with respect to V:
P=0.40⋅V−2/5
Using the power rule of differentiation, where ddx(xn)=nxn−1, we differentiate:
dPdV=0.40⋅(−25)V−2/5−1
This simplifies to:
dPdV=−0.805V−7/5=−0.16V7/5
Now, we need to evaluate this derivative at V=1m3:
dPdV∣∣∣V=1=−0.16(1)7/5=−0.16
The slope of the P-V curve at V=1m3 is:
dPdV=−0.16Pa/m3
Thus, the slope of the P-V curve at V=1m3 is −0.16 Pa/m³.
Topper's Solved these Questions
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Integration)
Explore 12 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Graphs))
Explore 30 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Trigonometry)
Explore 22 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
Similar Questions
An ideal gas follows a process PVγ = constant where γ = adiabatic exponent.The slope of P-V graph will be represented by
View SolutionAn ideal gas with the adiabatic exponent γ goes through a process p=p0−αV, where p0 and α are positive constants, and V is the volume. At what volume will the gas entropy have the maximum value ?
View Solution
Knowledge Check
An ideal gas is subjected to a cyclic process ABCD as depicted in the P-V diagram given below
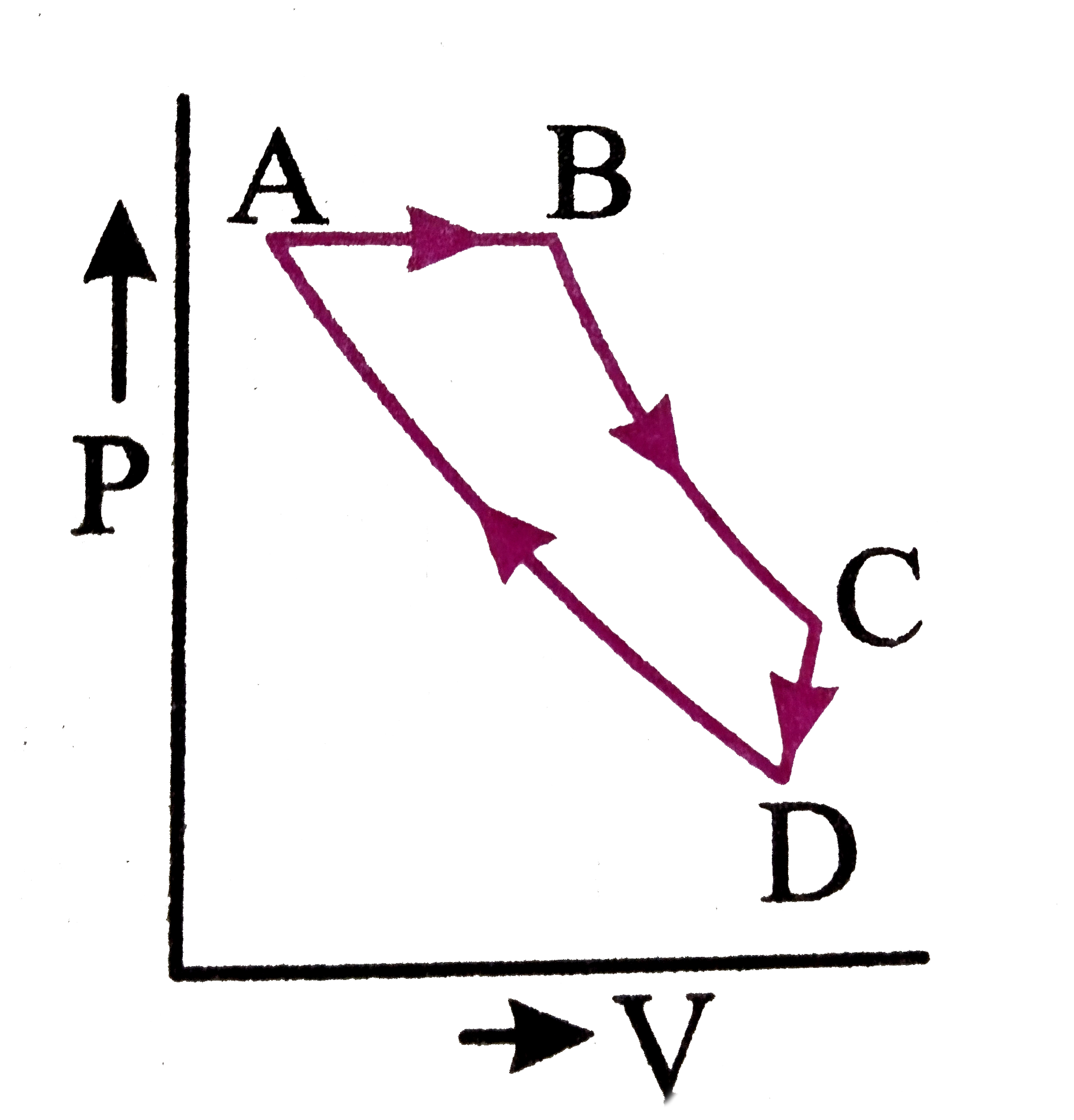
Which of the following curves represents the equivalent cyclic process?A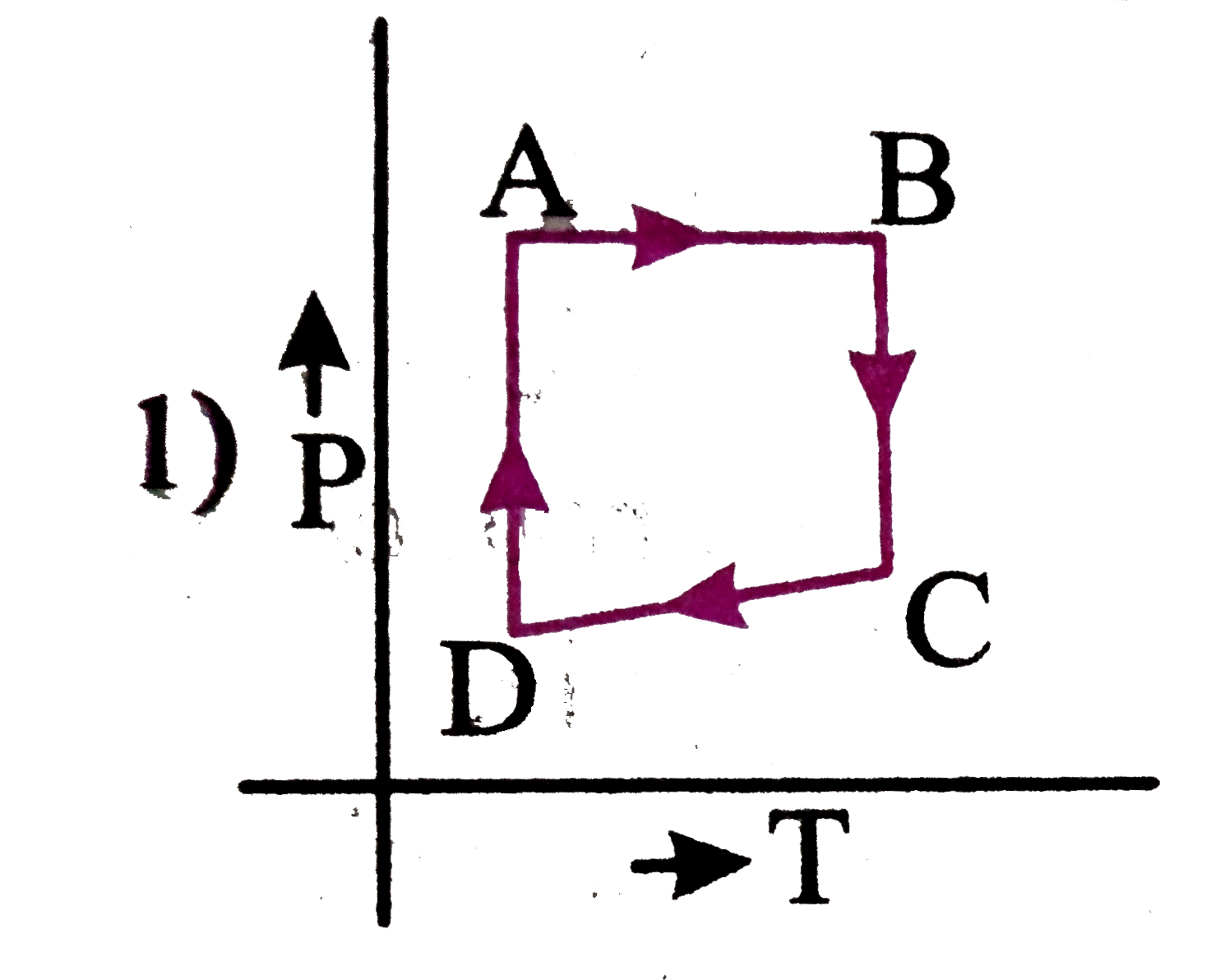 B
B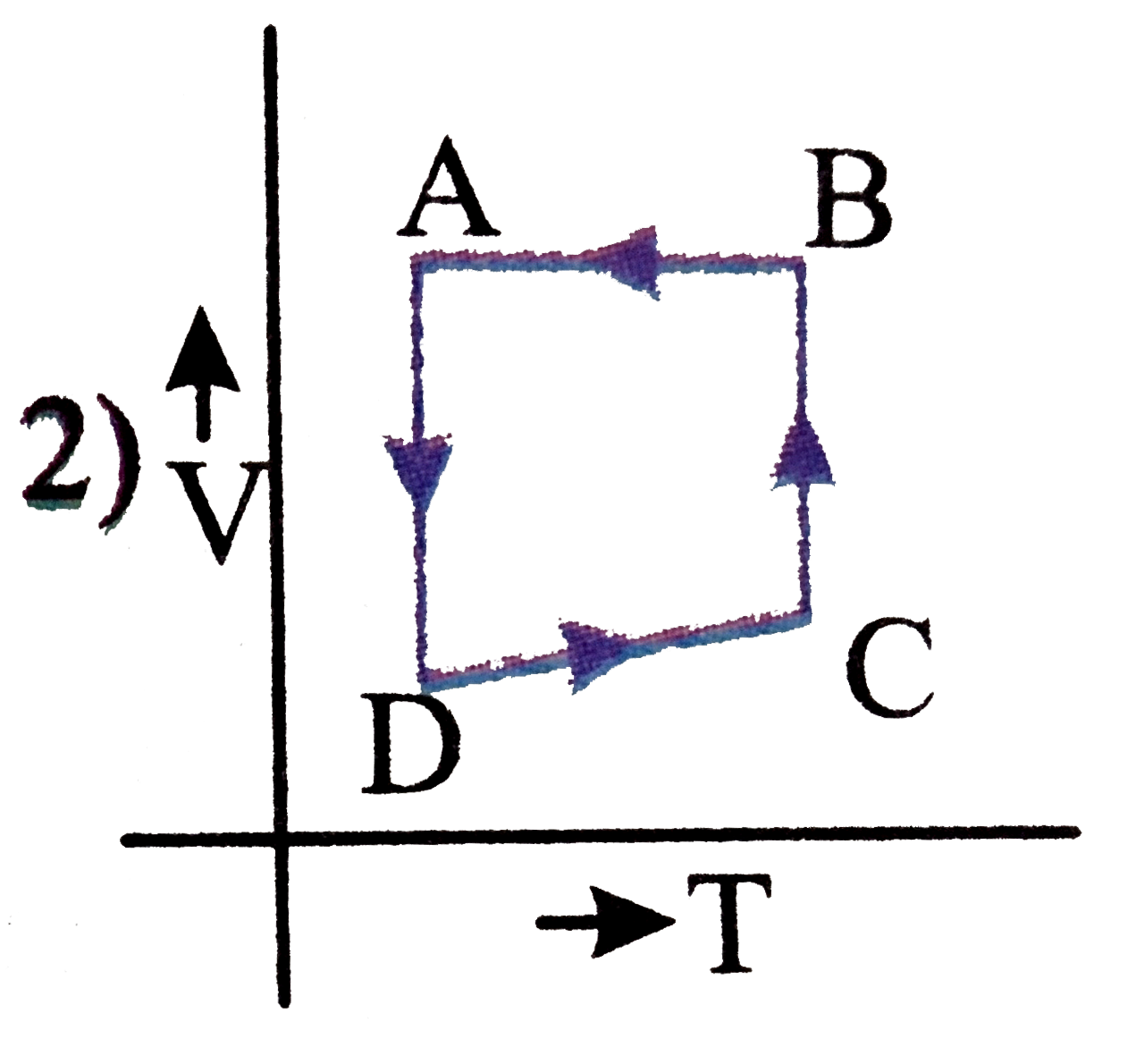 C
C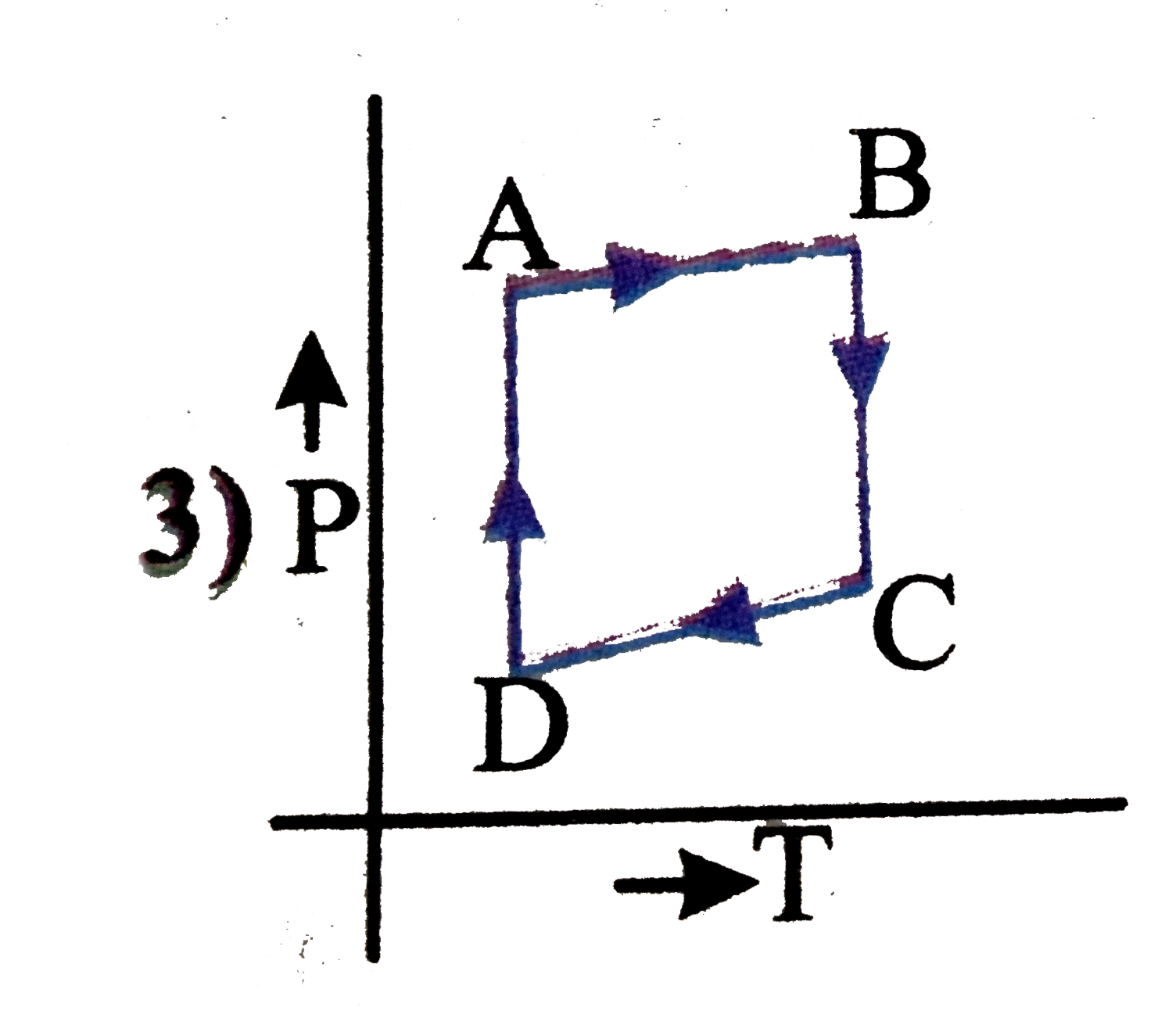 D
D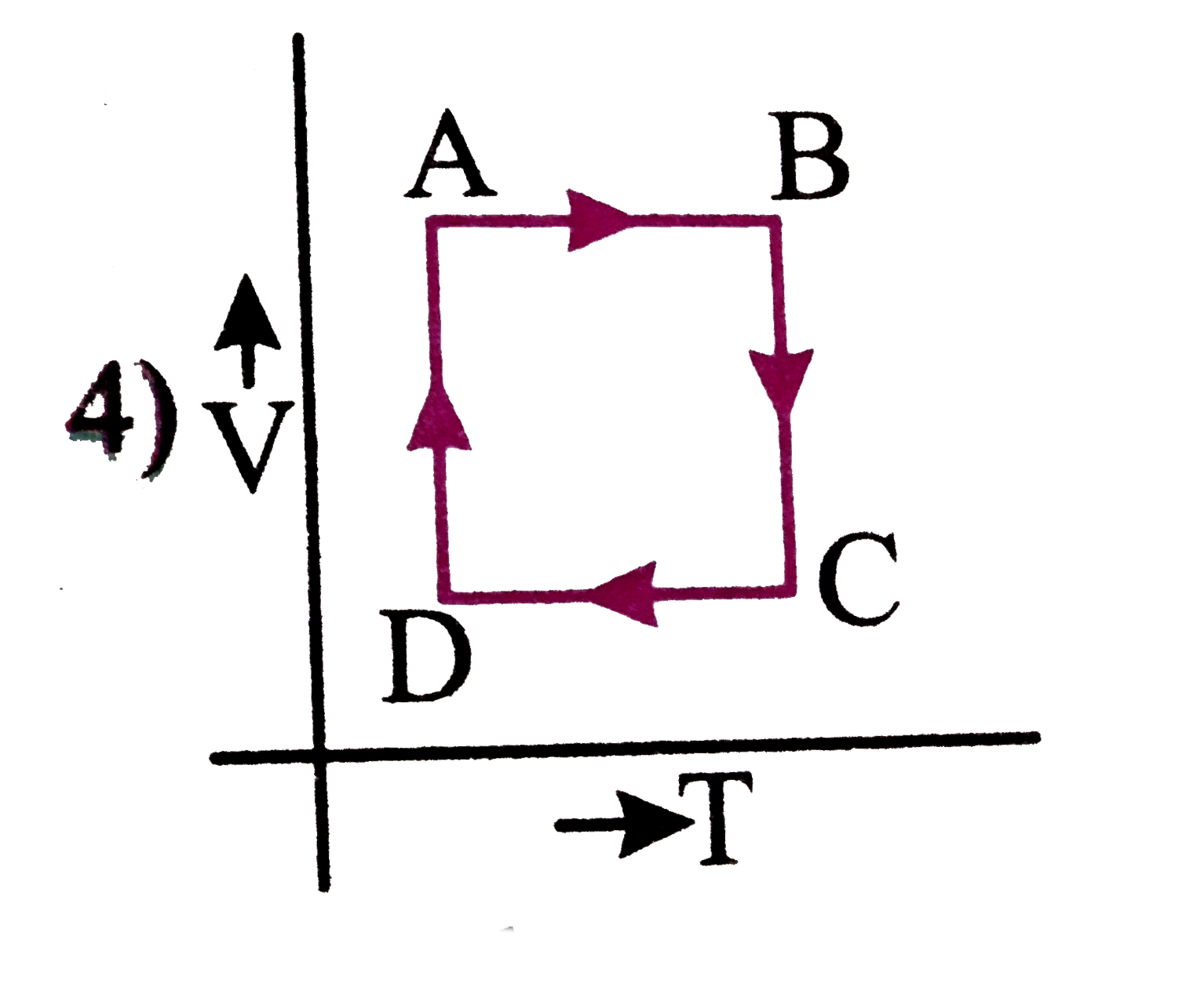
1 mol of an ideal gas undergoes different thermodynamical process in P−V diragram given below :

What will be the value of ΔH and ΔE for overall process ?AΔH=0BΔE=0CΔH=48.4 calorieDΔE=13.82 calorieOne mole of an ideal gas undergoes a process P=P0[1+(2V0V)2]−1, where P0V0 are constants. Change in temperature of the gas when volume is changed from V=V0→V=2V0 is:
A45P0V0nRB34P0V0nRC23P0V0nRD97P0V0nR
One mole. of an ideal gas undergoes a process P=P01+(V0V)2. Here P0 and V0 are constants. The change in temperature of the gas when volume is changed from V=V0 to V=2V0 is xP0V010R. Find x. (Here R= Universal gas constant)
View SolutionP-V graph for an ideal gas undergoing polytropic process PVm=constant is shown here. Find the value of m.
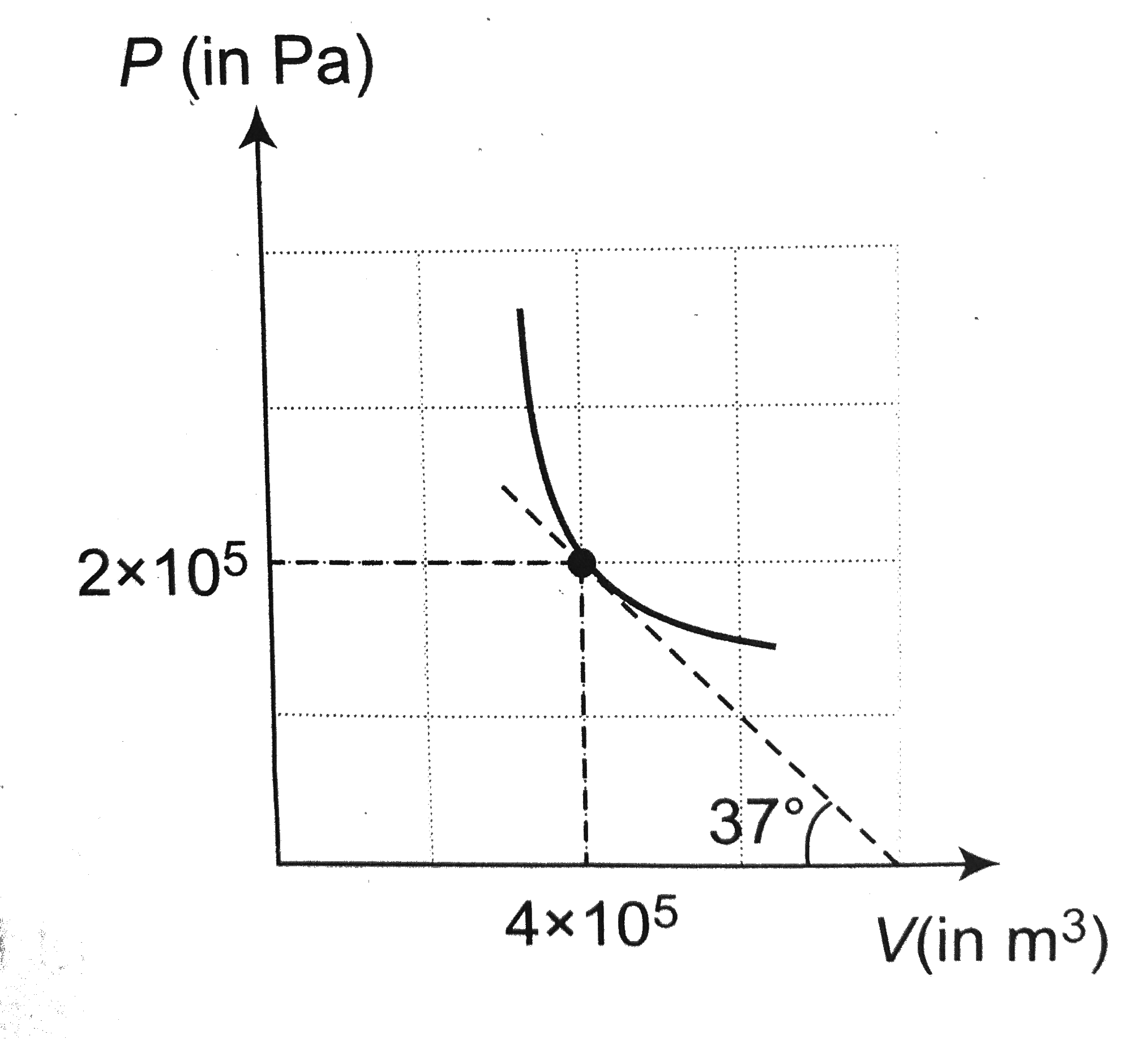
View SolutionA certain amount of an ideal monoatomic gas undergoes a thermodynamic process such that VT2= constat where V= volume of gas, T= temperature of gas. Then under process
View SolutionA certain balloon maintains an internal gas pressure of P0=100kPa until the volume reaches V0=20m3. Beyond a volume of 20m3, the internal pressure varies as P=P0+2k(V−V0)2 where P is in kPa. V is n m3 and k is a constant (k=1kPa/m3). Initially the balloon contains helium gas at 20∘C, 100kPa with a 15m3 volume. The balloon is then heated until the volume becomes 25m2 and the pressure is 159 kPa. Assume ideal gas behaviour for helium. The work done by the balloon for the entire process in kJ is
View SolutionOn P-V coordinates, the slope of an isothermal curve of a gas at a pressure P = IMPa and volume V= 0.0025 m3 is equal to −400Mpa/m3. If Cp/Cv=1.4 , the slope of the adiabatic curve passing through this point is :
View Solution

