Statement 1 : For very small angle , we may use approximation theta, the hypotenuse and the base become approximately of the same length.
(1) Statement-1 is True, Statement-2 is True,
Statement-2 is a correct explanation for
Statement-1.
Statement-1 is True, Statement-2 is True,
Statemen-2 is not a correct explanation for
Statement-1
Statement-1 is True, Statement-2 is False.
Statemen-1 is False, Statement-2 is True.
The correct Answer is:A
Step by step video, text & image solution for Statement 1 : For very small angle theta, we may use approximation sintheta ~~theta~~tantheta. and Statement 2 : For very small angle theta, the hypotenuse and the base become approximately of the same length. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Differentiation)
Explore 40 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Integration)
Explore 12 Videos
- RACEBook:ALLENChapter:RACEExercise:PHYSICS
Explore 10 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
Similar Questions
Knowledge Check
Assertion:− For a very small ∠θ ,sinθ≈θ.
Reason :−At very small angle, arc, subtends a right angle at the centre of arc.AIf both Assertion & Reason are True & the Reason is a correct explanation of the Assertion.BIf both Assertion & Reason are True but Reason is not a correct explanation of the Assertiion.CIf Assertion is True but the Reason is False.DIf both Assertion & Reason are FalseFor any angle theta, the expression 2cos8θ+12cosθ+1 is equal to
A(2cosθ+1)(2cos2θ+1)(2cos4θ+1)B(cosθ−1)(cos2θ−1)(cos4θ−1)C(2cos0−1)(2cos2θ−1)(2cos4θ−1)D(2cosθ+1)(2cos2θ+1)(cos4θ+1)Statement-1: f(θ)=sin2θ+cos2θ
then f(θ)=1 for every real values of θ.
Statement:2: g(θ)=sec2θ−tan2θ.
then g(θ)=1 for every real value of θ.
Statement-3: f(θ)=g(θ) for every real value of θ.ATFFBTTTCTFTDTTF
A right angled triangle has legs 1 and x. The hypotenuse is y and angle opposite to the side x is θ. Shown as
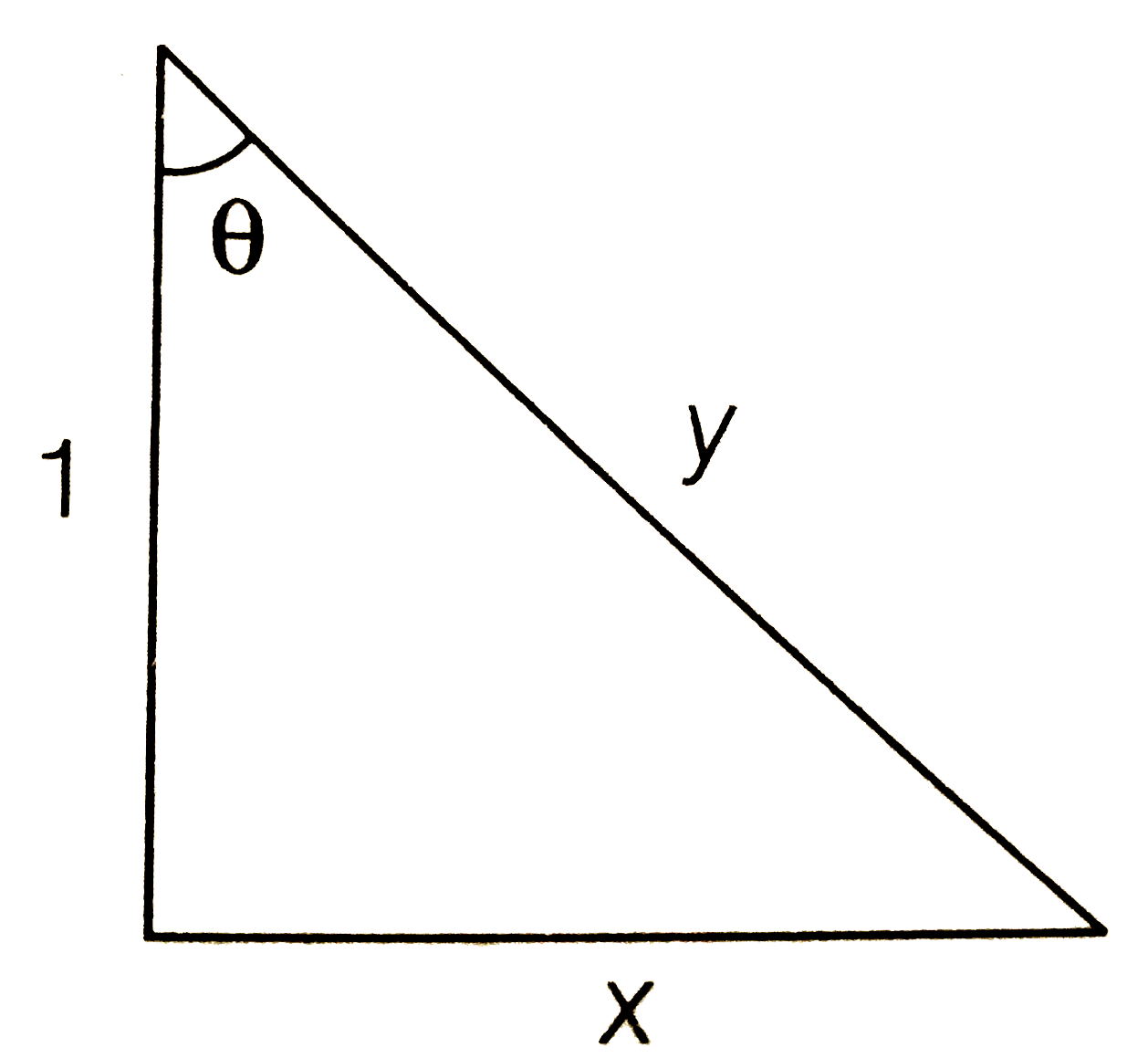

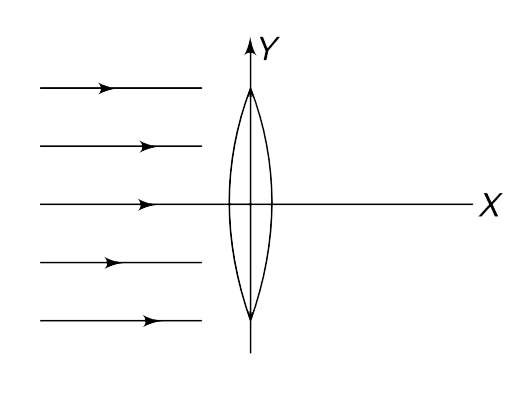
View SolutionMonochromatic light rays parallel to the principal axis (the x axis) are incident on a convex lens of focal length f. If the lens oscillates such that it tilts up to a small angle θ on either side of the y axis, then find the distance between the exterme positions of the image. Take secθ≈1+θ22 for small θ.
View SolutionIf the angle between the vectors a and b be θanda⋅b=cosθ then the true statement is
View SolutionFor the every θ,0<θ≤90, find the values of the following angle
2sin2θ−3sinθ=−1
View SolutionThe smallest positive angle θ satisfying the equation sin2θ−2cosθ+(1/4)=0 is
View Solution
