Infinite particles each of mass 'M' are placed at positions x=1m,x=2m,x=4m....∝. Find the gravitational field intensity at the origin.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_2_C05_S01_009_Q01.png" width="80%"gt
Video Solution
Text Solution
→Inet=→I1+→I2+→I3+→I4+...∞ terms
=GM(1)2ˆi+GM(2)2ˆi+GMˆi(4)2+....∞ terms =GMˆi(1+14+116+...∞) [Here in the GP a = 1 and r=14]
So, →Inet=GMˆi⎡⎣11−14⎤⎦=GMˆi⎡⎢
⎢⎣1(34)⎤⎥
⎥⎦⇒→Inet=43GMˆi
|
Topper's Solved these Questions
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:BOX-1
Explore 3 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:BOX-2
Explore 12 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:Exercise 5 B (Previous Year Questions)
Explore 9 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:subjective
Explore 14 Videos
- KINEMATICS-2DBook:ALLENChapter:KINEMATICS-2DExercise:Exercise (O-2)
Explore 48 Videos
Similar Questions
Match the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionIdentify the cell organelle 'A' :-

View SolutionMatch the following lists:

View SolutionFor shown situation find ∠BCA :-

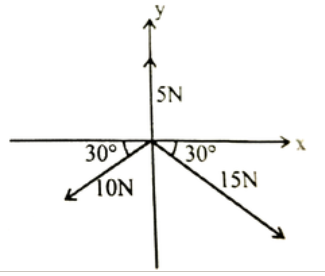
View SolutionFind the magnitude of the resultant of shown forces :-
View SolutionAt x=0, value of dydx is :

View SolutionThe equation of straight line shown in figure is :

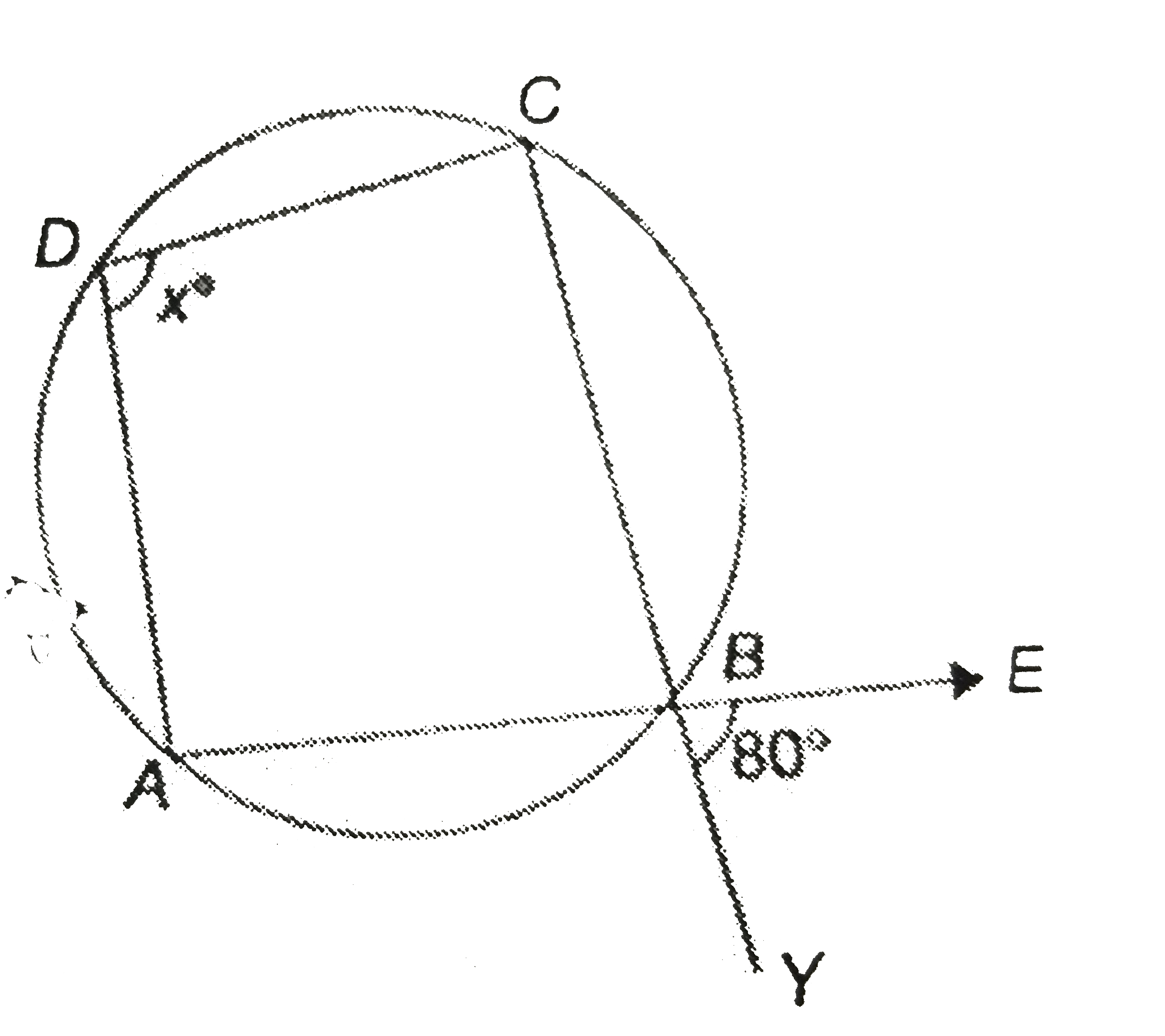
View SolutionIn Fig, find the value of x.
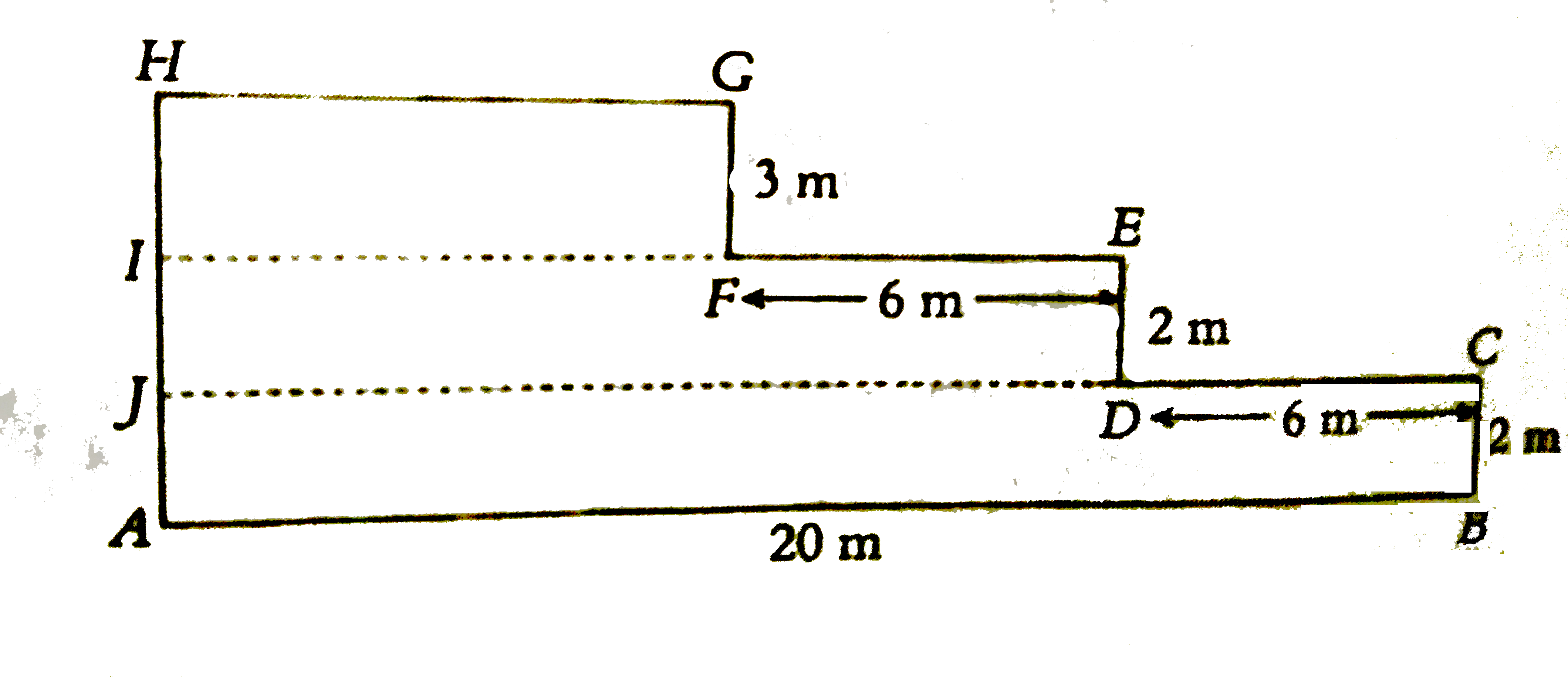
View SolutionFind the area of figure given below.
View Solution