Question

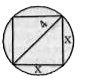
A square is incribed in a quarter circle in such a way that two of its adjacent vertices on the radius are equidistant from the centre and other two vertices lie on the circumference. If the side of square is $\sqrt{\frac{5}{2}}$ cm, then what is the radius (in cm) of the circle ?

Options

A. 2
B. `2.5`
C. 5
D. 10

Answer

B

Explanation

To solve the problem, we need to find the radius $$R$$ of a quarter circle in which a square is inscribed. The side length of the square is given as $$\sqrt{\frac{5}{2}}$$ cm.

1. Understanding the Geometry:
- We have a quarter circle with a square inscribed in it.
- Let the vertices of the square be \( A, B, C, D \) such that \( A \) and \( B \) are on the radius of the quarter circle, and \( C \) and \( D \) are on the arc of the quarter circle.

2. Identifying the Side Length:
- The side length of the square \( AB = BC = CD = DA = \sqrt{\frac{5}{2}} \) cm.

3. Finding the Diagonal of the Square:
- The diagonal \( BD \) of the square can be calculated using the Pythagorean theorem:
\( BD = \sqrt{AB^2 + AD^2} = \sqrt{\left(\sqrt{\frac{5}{2}}\right)^2 + \left(\sqrt{\frac{5}{2}}\right)^2} \)
- Simplifying this gives:
\( BD = \sqrt{\frac{5}{2} + \frac{5}{2}} = \sqrt{5} \)

4. Analyzing Triangle \( BOD \):
- In triangle \( BOD \), where \( O \) is the center of the quarter circle, we have:
- \( \angle BOD = 90^\circ \) (since it's a quarter circle).
- \( \angle OBD = 45^\circ \) (since \( BD \) bisects the right angle of the square).
- Therefore, \( \angle ODB = 45^\circ \) as well.

5. Using the Pythagorean Theorem in Triangle \( BOD \):
- By the Pythagorean theorem:
\( BO^2 + OD^2 = BD^2 \)
- Here, \( BO = R \) (the radius we want to find) and \( OD = \frac{\sqrt{5}}{2} \) (half the diagonal of the square):
\( R^2 + \left(\frac{\sqrt{5}}{2}\right)^2 = (\sqrt{5})^2 \)
- Simplifying this:
\( R^2 + \frac{5}{4} = 5 \)
- Rearranging gives:
\( R^2 = 5 - \frac{5}{4} = \frac{20}{4} - \frac{5}{4} = \frac{15}{4} \)

6. Finding the Radius:
- Taking the square root:
\( R = \sqrt{\frac{15}{4}} = \frac{\sqrt{15}}{2} \)

7. Final Calculation:
- To express \( R \) in decimal form:
\( R \approx \frac{3.872}{2} \approx 1.936 \text{ cm} \)

Conclusion:
The radius \( R \) of the quarter circle is approximately \( 1.936 \) cm.