Figure shows two light rays that are initially exactly in phase and that reflect from several glass surfaces. Neglect the slight slant in the path of the light in the second arrangement. The path length difference in terms of wavelength λ is :
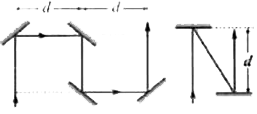
2d
(d+λ)
(2d+λ)
none of these
The correct Answer is:C
x1=5d+4×λ/2=5d+2λ
and x2=3d+2×λ2=3d+λ
∴ Δx=x1~x2=(5d+2λ)−(3d+λ)=(2d+λ).
Topper's Solved these Questions
- WAVE OPTICSBOOK - DISHA PUBLICATIONCHAPTER - WAVE OPTICSEXERCISE - EXERCISE-1 : CONCEPT BUILDER
65 Videos
- THERMODYNAMICS BOOK - DISHA PUBLICATIONCHAPTER - THERMODYNAMICS EXERCISE - EXERCISE -2 : CONCEPT APPLICATOR
29 Videos
- WAVESBOOK - DISHA PUBLICATIONCHAPTER - WAVESEXERCISE - EXERCISE -2 CONCEPT APPLICATOR
30 Videos
Similar Questions
The diffraction pattern of a single slit is shown in the figure. The point at which the path difference of the extreme rays is two times the wavelength is

View SolutionShow using a proper diagram how unpolarised light can be linearly polarised by reflection from a transparent glass surface.
View Solution
Knowledge Check
In the figure shown, light waves A and B both of wavelength λ are initially in phase and travelling rightward as incident by the two rays. Wave A is reflected from four parallel surfaces but ends up travelling in original direction. The possible value(s) of distance L in terms of wavelength λ in figure which put A and B exactly out of phase with each other after all the reflected is/are
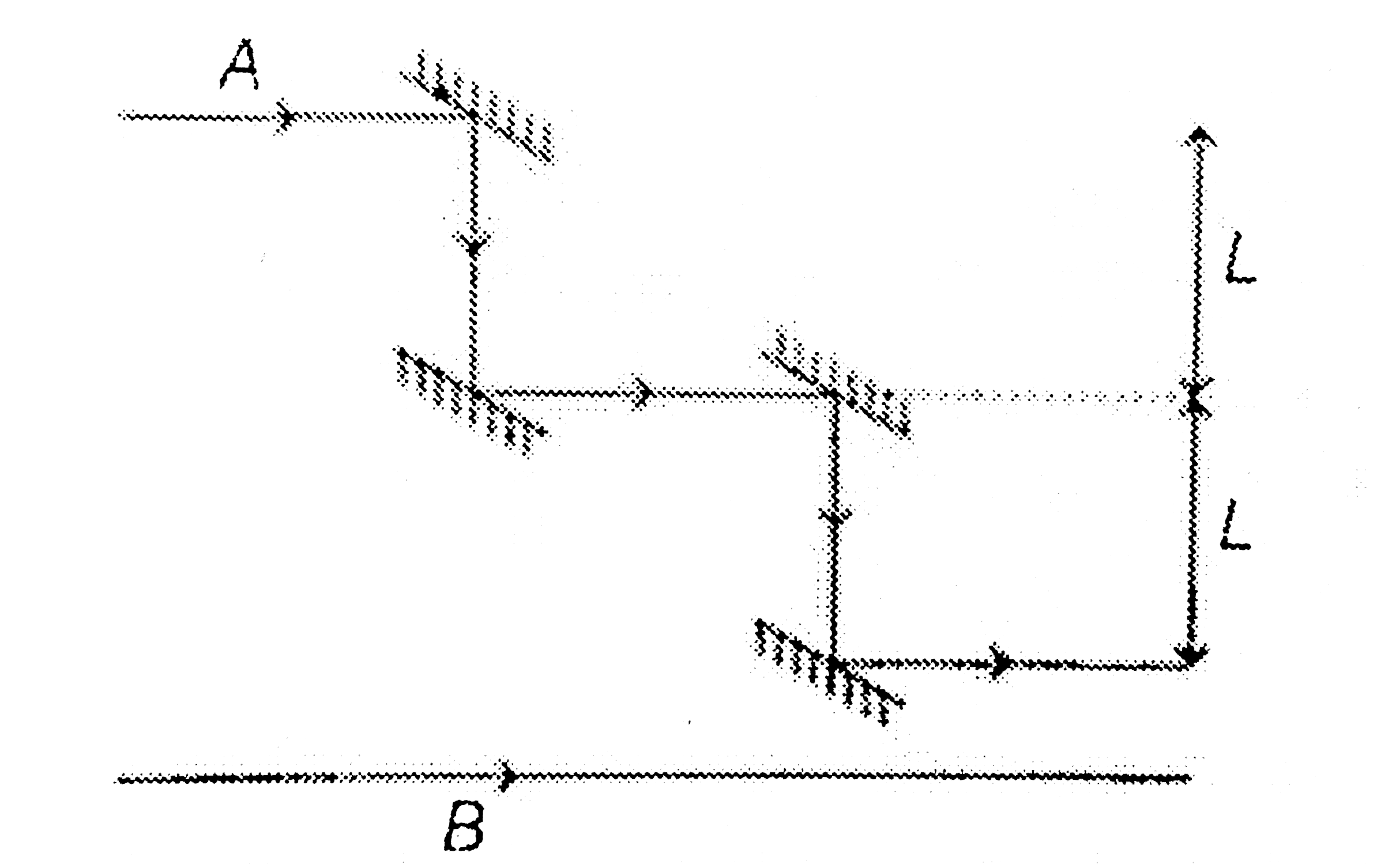 Aλ/2B3λ/2C3λ/4Dλ
Aλ/2B3λ/2C3λ/4DλA point source of light is placed in front of a plane mirror as shown in Figure.
Determine the length of reflected path of light on the screen Σ
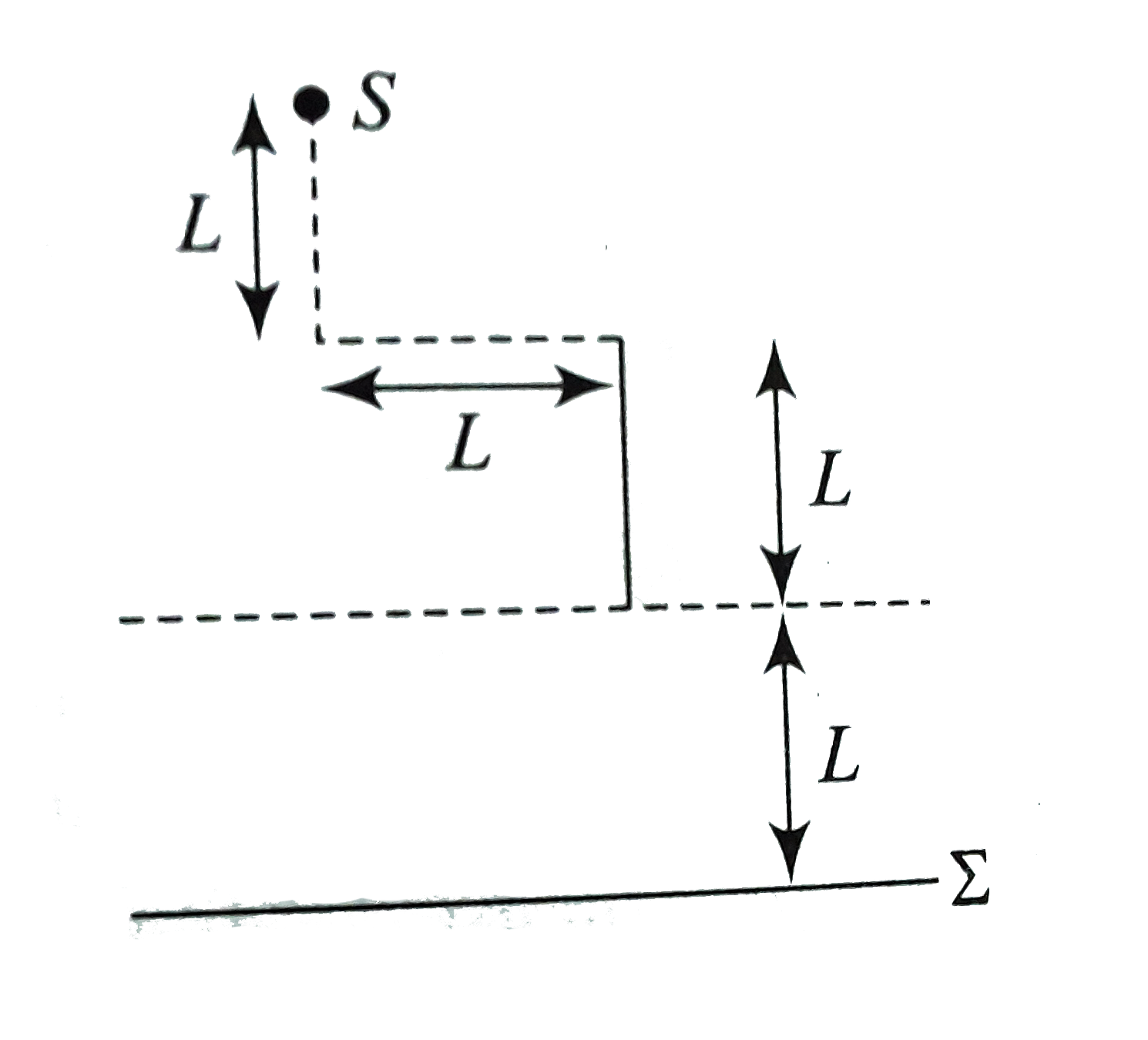 ALB2LC3L/2DL/2
ALB2LC3L/2DL/2A ray of light passing through A retraces its path on reflection from a concave mirror. If PA=30cm, what is the focal length of the mirror ?
A60cmB20cmC30cmD15cm
Show using a proper diagram how unpolarised light can be linearly polarised by reflection from a transparent glass surface.
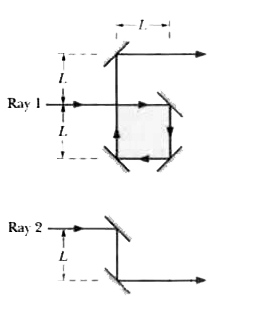
View SolutionIn Figure, two light rays go through different paths by reflecting from the various flat surfaces shown. The light waves have a wavelength of 411.0 nm and are initially in phase. What are the (a) smallest and (b) second smallest value of distance L that will put the waves exactly out of phase as they emerge from the region?
View SolutionLight of wavelength λ in air enters a medium of refractive index μ. Two points in this medium, lying along the path of this light, are at a distance x apart. The phase difference between these points is :
View SolutionLight of wavelength λ in air enters a medium of refractive index μ. Two points in this medium, lying along the path of this light, are at a distance of x apartThe phase difference between these point is
View SolutionA light ray incidents on water (n=43) surface from air and reflected from air and reflected part of it is found to be polarized. Find the deviation of refracted light from its original path:
View Solution
