For a series RLC circuit R=XL=2XC. The impedence of the current and phase different (between) V and i will be
√5R2,tan−1(2)
√5R2,tan−1(12)
√5XC,tan−1(2)
√5R,tan−1(12)
The correct Answer is:B
R=XL=2XC
Z=√R2+(XL−XC)2=√(2X2C+(2XC−XC)2
=√(4X2c)+X2C
=√(4X2c)+X2C
=√5XC=√5R2
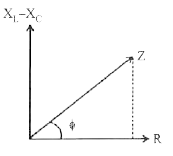
tanϕ=XL−XCR=2XC−XC2XC
tanϕ=12,ϕ=tan−1(12)
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - DISHA PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - Exercise - 1 : CONCEPT BUILDER (Topic 3 : Transformers and LC Oscillations)
19 Videos
- ALTERNATING CURRENT BOOK - DISHA PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - Exercise -2 : Concept Applicator
30 Videos
- ALTERNATING CURRENT BOOK - DISHA PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - Exercise - 1 : CONCEPT BUILDER (TOPIC 1: Alternating Current, Voltage and Power)
20 Videos
- ATOMSBOOK - DISHA PUBLICATIONCHAPTER - ATOMSEXERCISE - EXERCISE-2: CONCEPT APPLICATOR
30 Videos
Similar Questions
Knowledge Check
For a series RLC circuit R=XL=2XC. The impedance of the current and phase different (between) V and i will be
A√5R2,tan−1(2)B√5R2,tan−1(12)C√5XC,tan−1(2)D√5R,tan−1(12)In an AC circuit XC=XL. The phase differe3nce between the current and voltage will be
A0BπCπ/2Dπ/4In a series LCR circuit, resistance R=10Ω and the impedence Z=20Ω the phase difference between the current and the voltage is
A30∘B45∘C60∘D90∘
In a series LCR circuit, VL=VC≠VR. What is the value of power factor ?
View SolutionIn a series LCR circuit resistance R=10Ω and the impedance Z=10Ω The phase difference between the current and the voltage is
View SolutionIn a series A.C. circuit , R=100Ω, XL=300Ω and XC=200Ω. The phase difference between the applied e.m.f. and the current will be
View SolutionIn a series LCR circuit, resistance R = 10 Ω and the impedance z = 20 Ω . The phase difference between the current and voltage is
View SolutionA sinusoidal voltage of peak value 283 V and angular frequency 320/s is applied to a series LCR circuit.Given that R=5Ω,L=25mH and C=1000μF.The total impedance, and phase difference between the voltage across the source and the current will respectively be:
View Solution