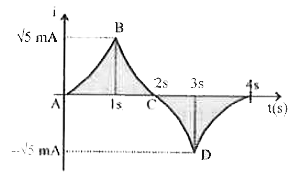
Figure shows one cycle of an alternating current with the segments AB,

The root mean square value of the alternating current is equal to
ATwice the peak value
BHalf the peak value
C $\frac{1}{\sqrt{2}}$ times the peak value
DEqual to the peak value
The average value of alternating current over a complete cycle is
Azero
B1 rms
C $\frac{I}{\sqrt{2}}$
D $2 I$
The equation of an alternating current is $I = 50 \sqrt{2} sin 400 π t A$ , then the frequency and the root mean square value of current are respectively.
A $200 H z, 50 A$
B $400 H z, 50 \sqrt{2} A$
C $200 H z, 50 \sqrt{2} A$
D $500 H z, 200 A$

Figure shows one cycle of an alternating current with the segments AB, BC, CD, DE being symmetrical and parabolic. The root mean square value of this current over one cycle is x mA, find x.