A copper wire of length 40cm, diameter 2mm and resistivity 1.7×10−8Ωm forms a square frame. If a uniform magnetic field B exists in a direction perpendicular to the plane of square frame and it changes at a steady rate dBdt=0.02 T/s, then find the current induced in the frame.
9.3×10−2 amp
9.3×10−1 amp
3.3×10−2 amp
19.3×10−2 amp
The correct Answer is:A
To solve the problem step by step, we will follow these steps:
Step 1: Convert Given Measurements
- Length of the copper wire: L=40cm=0.4m
- Diameter of the wire: d=2mm=0.002m
- Radius of the wire: r=d2=0.0022=0.001m
- Resistivity of copper: ρ=1.7×10−8Ωm
Step 2: Calculate the Area of the Square Frame
Since the wire forms a square frame, the total length of the wire is equal to the perimeter of the square frame.
- Perimeter of the square frame: P=4a where a is the side length.
- Therefore, a=L4=0.44=0.1m
Now, calculate the area A of the square frame:
A=a2=(0.1m)2=0.01m2
Step 3: Calculate the Induced EMF
The induced EMF E can be calculated using the formula:
E=−dΦdt
Where Φ is the magnetic flux given by:
Φ=B⋅A
Since A is constant, we have:
E=A⋅dBdt
Substituting the values:
- A=0.01m2
- dBdt=0.02T/s
Thus,
E=0.01⋅0.02=2×10−4V
Step 4: Calculate the Resistance of the Wire
The resistance R of the wire can be calculated using the formula:
R=ρLAw
Where Aw is the cross-sectional area of the wire given by:
Aw=πr2
Calculating Aw:
Aw=π(0.001)2=π×10−6≈3.14×10−6m2
Now substituting the values into the resistance formula:
R=(1.7×10−8)⋅(0.4)3.14×10−6
R≈6.8×10−93.14×10−6≈2.16×10−3Ω
Step 5: Calculate the Induced Current
Using Ohm's law, the induced current I can be calculated as:
I=ER
Substituting the values:
I=2×10−42.16×10−3
I≈9.26×10−2A
Final Answer
The induced current in the frame is approximately:
I≈0.0926A
---
- Length of the copper wire: L=40cm=0.4m
- Diameter of the wire: d=2mm=0.002m
- Radius of the wire: r=d2=0.0022=0.001m
- Resistivity of copper: ρ=1.7×10−8Ωm
Since the wire forms a square frame, the total length of the wire is equal to the perimeter of the square frame.
- Perimeter of the square frame: P=4a where a is the side length.
- Therefore, a=L4=0.44=0.1m
A=a2=(0.1m)2=0.01m2
The induced EMF E can be calculated using the formula:
E=−dΦdt
Where Φ is the magnetic flux given by:
Φ=B⋅A
Since A is constant, we have:
E=A⋅dBdt
- A=0.01m2
- dBdt=0.02T/s
E=0.01⋅0.02=2×10−4V
The resistance R of the wire can be calculated using the formula:
R=ρLAw
Where Aw is the cross-sectional area of the wire given by:
Aw=πr2
Aw=π(0.001)2=π×10−6≈3.14×10−6m2
R=(1.7×10−8)⋅(0.4)3.14×10−6
R≈6.8×10−93.14×10−6≈2.16×10−3Ω
Using Ohm's law, the induced current I can be calculated as:
I=ER
Substituting the values:
I=2×10−42.16×10−3
I≈9.26×10−2A
The induced current in the frame is approximately:
I≈0.0926A
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION Book:DISHA PUBLICATIONChapter:ELECTROMAGNETIC INDUCTION Exercise:EXERCISE - 1 : Concept Builder
Explore 68 Videos
- ELECTRIC CHARGES AND FIELDS Book:DISHA PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:Exercise - 2 : Concept applicator
Explore 24 Videos
- ELECTROMAGNETIC WAVESBook:DISHA PUBLICATIONChapter:ELECTROMAGNETIC WAVESExercise:Exercise - 2 : Concept Applicator
Explore 30 Videos
Similar Questions
A uniform magnetic field B exists in a direction perpendicular to the palne of a square frame made of copper wire. The wire has a total length of 40cm . The magnetic field changes with time at a steady rate (dB/dt)=0.02T/sec . Find the current induced in the frame. Resistance of wire =I0Ω
View SolutionA uniform magnetic field B exists in a direction perpendicular to the plane of a square frame made of copper wire. The wire has a diameter of 2 mm and a total length of 40cm. The magntic field changes with time at a steady rate dBdt=0.02Ts−1.F∈dthecurrent∈duced∈theame.Resistivityofcopper=1.7 X 10 ^(-8) Wm.
View Solution
Knowledge Check
A copper wire of length 40 cm, diameter 2mm and resistivity 1.7×10−8Ωm form a square frame. If a uniform magnetic field B exists in a direction perpendicular to the plane of square frame and it changes at a steadyrate dBdt=0.02 T/s, then find the current induced in the frame.
A9.3×10−2 amp(b)B9.3×10−1 ampC3.3×10−2 amp(d)D19.3×10−2 ampA uniform magnetic field B exists in a cylindrical region of radius I0cm as shown in figure. A uniform wire or length 80cm and resistance 44.0Ω is bent into a square frame and is placed with one side along a diameter of the cylindrical region. if the magnetic field increases at a constant rate of 0.0I0T/sec , the current induced in the frame
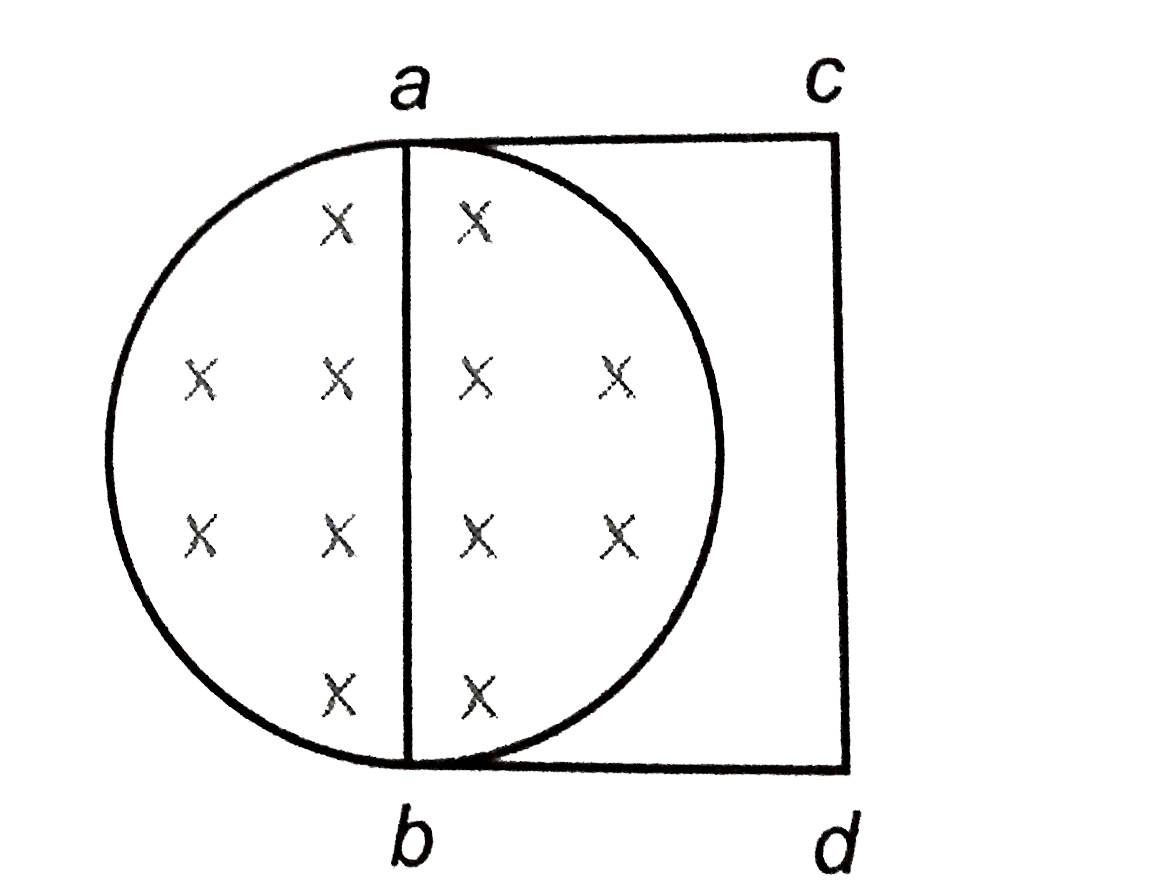 A3.9×10−5AB4.0×10−5AC4.1×10−5AD3.9×10−4A
A3.9×10−5AB4.0×10−5AC4.1×10−5AD3.9×10−4AIn a coil of area 10cm2 and 10 turns, magnetic field is directed perpendicular to the plane and is changing at a rate of 104Ts−1. The resistance of the coil is 20Ω. The current in the coil will be
A0.5 AB0.20833333333333C5 AD5×108A
A square of side 2.0m is placed in a uniform magnetic field B=2.0T in a direction perpendicular to the plane of the square inwards. Equal current i=3.0A is flowing in the directions shown in figure. Find the magnitude of magnetic force on the loop.

View SolutionA current of 2A enters at the corner d of a square frame abcd of side 10cm and leaves at the opposite corner b.A magnetic field B=0.1T exists in the space in direction perpendicular to the plane of the frame as shown in figure.Find the magnitude and direction of the magnetic forces on the four sides of the frame.
View SolutionA unifrom magnetic field B exists in a cylindrical region of radius 1 cm as shown in figure. A uniform wire of length 16 cm and resistance 4.0Ω is bent into a square frame and is placed with one side along a diameters of the cylindrical region. If the magnetic field increaes at a constant rate of 1 T/s find the current induced in the frame.
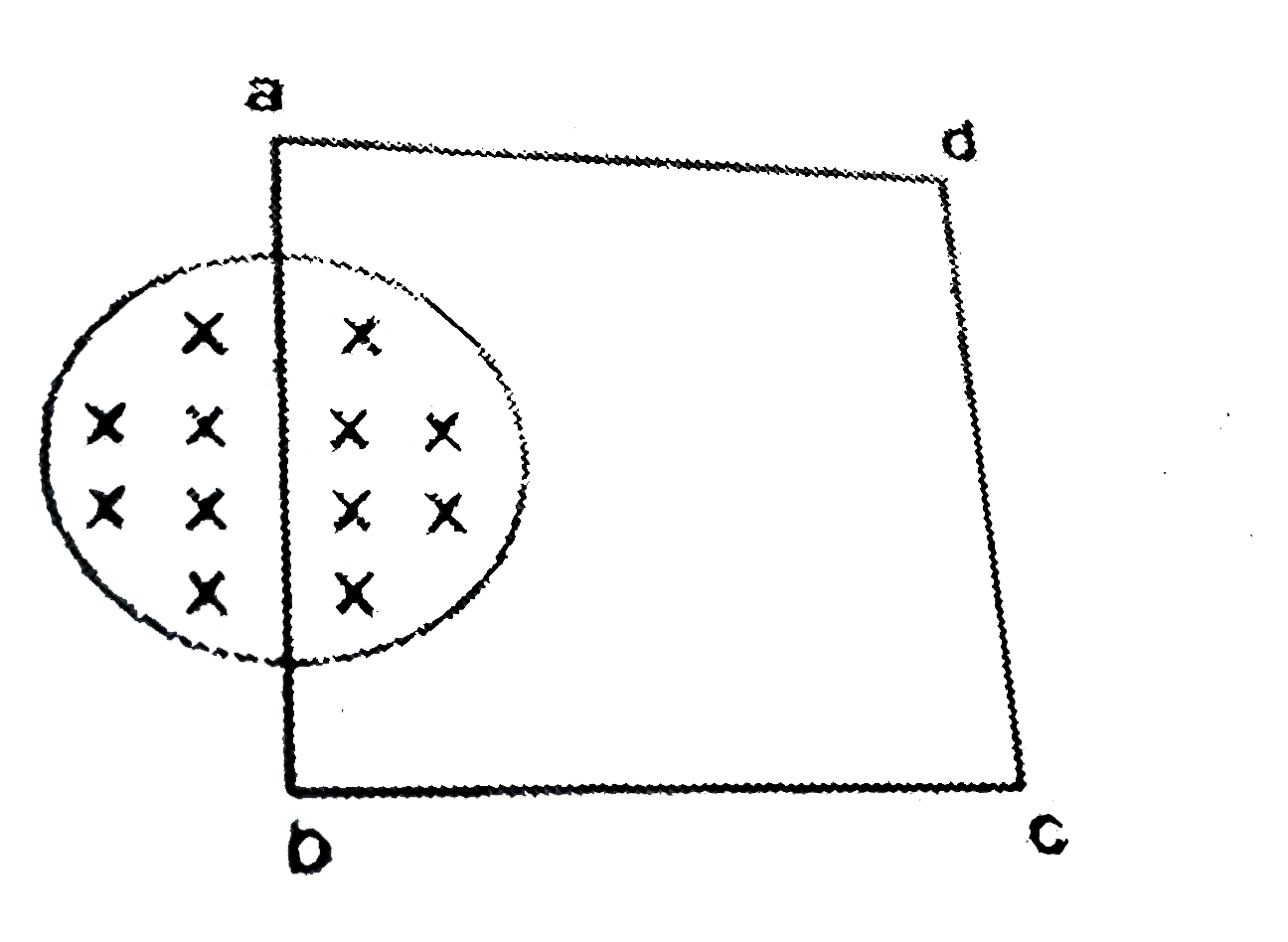
View SolutionA copper wire bent in the shape of a semicircle of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the direction perpendicular to the plane of the wire. Find the emf induced between the ends of the wire if (a) the velocity is perpendicular ot the diameter joining free ends, (b) the velocity is parallel to this diameter.
View SolutionA copper wire of length 50.0 cm and total resistance of 1.1×10−2Ω is formed into a circular loop and placed perpendicular to a uniform magnetic field that is increasing at the constant rate of 10.0 mT/s. At what rate is thermal energy generated in the loop?
View Solution

