The magnetic flux through a circuit of resistance R changes by an amount in a time . Then the total quantity of electric charge Q that passes any point in the circuit during the time is represented by
A
B
C
D
Video Solution
Text Solution
The correct Answer is:C
|
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION BOOK - DISHA PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - EXERCISE - 2 : Concept Applicator
29 Videos
- ELECTROMAGNETIC INDUCTION BOOK - DISHA PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - EXERCISE - 2 : Concept Applicator
29 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - DISHA PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Exercise - 2 : Concept applicator
24 Videos
- ELECTROMAGNETIC WAVESBOOK - DISHA PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise - 2 : Concept Applicator
30 Videos
Similar Questions
Knowledge Check
The magnetic flux through a circuit of resistance R changes by an amount Δϕ in a time Δt. Then the total quantity of electric charge Q that passes any point in the circuit during the time Δt is represent by
AQ=1r.ΔϕΔtBQ=ΔϕRCQ=ΔϕΔtDQ=(R).ΔϕΔtThe magnetic flux through a circuit of resistance R changes by an amount Adg in time At. The total quantity of electric charge Q, which is passing during this time through any point of the circuit is given by
AQ=ΔϕBΔtBQ=ΔϕBΔt.RCQ=−(ΔϕB))Δt.1RDQ=−ΔϕBRA magnetic flux through a stationary loop with a resistance R varies during the time interval τ as ϕ=at(τ−t). Find the amount of the generated in the loop during that time
Aaτ22RBa2τ23RC2a2τ33RDaτ3R
A magentic flux through a statinary loop with a resistance R varies during the tiem interval τ as Φ=at(τ−t). Find the amount of heat generated in the loop during that time. The inductance of the loop is to be neglected.
View SolutionThe charge q in the circuit shown here varies with time t as :
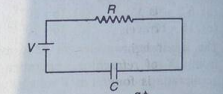
View SolutionThe charge q in the circuit shown here varies with time t as :

View SolutionThe magnetic flux through a stationary loop with resistance R varies during interval of time T as ϕ = at (T – t). The heat generated during this time neglecting the inductance of loop will be
View SolutionThe charge flowing through a resistance R varies with time tasQ=at−bt2. The total heat produced in R is
View Solution