An air capacitor of capacity C=10μF is connected to a constant voltage battery of 12V. Now the space between the plates is filled with a liquid of dielectirc constant 5. The charge that flows now from battery to the capacitor is
120μC
600μC
480μC
24μC
The correct Answer is:C
q1=C1V=10×12=120μC
q2=C2V=KC1×V=5×10×12=600μC
Additional charge that flows
=q2−q1=600−120=480μC
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - DISHA PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - EXERCISE 2: CONCEPT APPLICATOR
24 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - DISHA PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - EXERCISE 2: CONCEPT APPLICATOR
24 Videos
- ELECTROMAGNETIC WAVESBOOK - DISHA PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise - 2 : Concept Applicator
30 Videos
- GRAVITATIONBOOK - DISHA PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - EXERCISE-2
30 Videos
Similar Questions
A cell of voltage V0 is connected across a capacitor of capacitance C. Now the space between the plates is filled with a material of dielectric constant K. Find ratio of charge appear on the plates of capacitor before and after filling.
View SolutionA capacitor of some capacitance is charged by a 12V battery.Now the space between the plates of capacitors is filled with a dielectric of dielectric constant K=0.5 and again it is charged. The magnitude of the charge will
View Solution
Knowledge Check
A parallel plate capacitor of capacitance 10μF is connected across a battery of emf 5 mV. Now, the space between the plates of the capacitors is filled with a deielectric material of dielectric constant K=5. Then, the charge that will flow through the battery till equilibrium is reached is
A250μCB250nCC200nCD200μCConsider a disconnected. Plate capacitor of capacity 10μ with air filled in the gap between the plates. Now one-half of the space between the plates is filled with a dielectric of dielectric constant 4 as shown in .The capacity of the capacitor changes to
 .A25μFB20μFC40μFD5μF
.A25μFB20μFC40μFD5μFConsider a parallel plate capacitor of 10μF with air filled in the gap between the plates. Now one half of the space between the plates is filled with a dielectric of dielectric constant 4, as shown in the figure. The capacity of the capacitor charges to
 A25μFB20μFC40μFD5μF
A25μFB20μFC40μFD5μF
A parallel plate capacitar, of capacitance, 20μF, is connected to a 100 V supply. After some time, the battery is disconnected , and the space, between the plates of the capacitor is filled with a dielectric, of dielectric constant 5. Calculate the energy stored in the capacitar (i) before (ii)after dielectric has been put in between its plates.
View SolutionA parallel plate condenser is charged by connected it to a battery. Without disconnected the battery, the space between the plates is completely filled with a medium of dielectric constant k. Then
View SolutionA capacitor with air as the dielectric is charged to a potential of 100 volts. If the space between the plates is now filled with a dielectric of dielectric constant 10, the potential difference between the plates will be
View SolutionAn air capacitor is charged to a potential of 150 V and then the charging battery is disconnected. If the space between the plates is then completely filled with a material of dielectric constant 10 , then the potential between the plates will become
View SolutionTwo identical parallel plate capacitors of capacitance C each are connected in series with a battery of emf, E as shown. If one of the capacitors is now filled with a dielectric of dielectric constant k, the amount of charge which will flow through the battery is (neglect internal resistance of the battery)
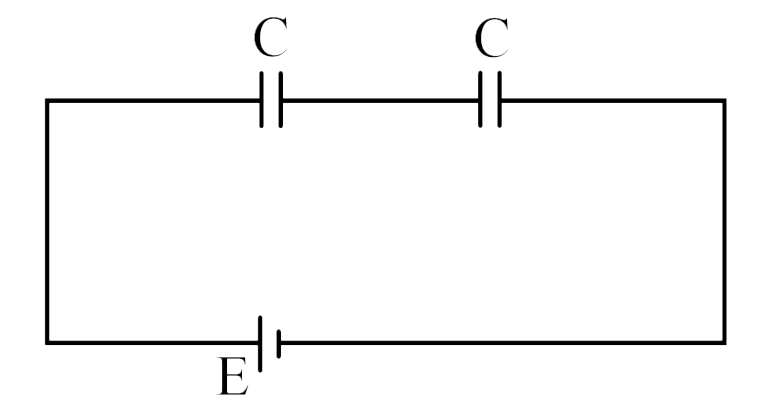
View Solution
