A cylindrical rod of aluminium is of length 20 cm and radius 2 cm. The two ends are maintained at temperatures of 0∘C and 50∘C the coefficient of thermal conductivity is 0.5 calcm×sec×∘C. Then the thermal resistance of the rod in calsec×∘C is
318
31.8
3.18
0.318
The correct Answer is:D
To find the thermal resistance of the cylindrical rod, we can use the formula for thermal resistance Rth:
Rth=Lk⋅A
where:
- L = length of the rod,
- k = coefficient of thermal conductivity,
- A = cross-sectional area of the rod.
Step 1: Identify the given values
- Length of the rod, L=20cm
- Radius of the rod, r=2cm
- Coefficient of thermal conductivity, k=0.5calcm⋅s⋅∘C
Step 2: Calculate the cross-sectional area A
The cross-sectional area A of a cylinder is given by the formula:
A=πr2
Substituting the radius:
A=π(2cm)2=π⋅4cm2
Using π≈3.14:
A≈3.14⋅4=12.56cm2
Step 3: Substitute the values into the thermal resistance formula
Now we can substitute the values of L, k, and A into the thermal resistance formula:
Rth=20cm0.5calcm⋅s⋅∘C⋅12.56cm2
Step 4: Calculate the denominator
Calculating the denominator:
0.5⋅12.56=6.28cals⋅∘C
Step 5: Calculate the thermal resistance
Now substituting this back into the equation for Rth:
Rth=206.28≈3.18cals⋅∘C
Final Answer
The thermal resistance of the rod is approximately:
Rth≈3.18cals⋅∘C
- L = length of the rod,
- k = coefficient of thermal conductivity,
- A = cross-sectional area of the rod.
- Length of the rod, L=20cm
- Radius of the rod, r=2cm
- Coefficient of thermal conductivity, k=0.5calcm⋅s⋅∘C
The cross-sectional area A of a cylinder is given by the formula:
Now we can substitute the values of L, k, and A into the thermal resistance formula:
Calculating the denominator:
Now substituting this back into the equation for Rth:
The thermal resistance of the rod is approximately:
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTER Book:DISHA PUBLICATIONChapter:THERMAL PROPERTIES OF MATTER Exercise:Exercise-2 (Concept Applicator)
Explore 28 Videos
- THERMAL PROPERTIES OF MATTER Book:DISHA PUBLICATIONChapter:THERMAL PROPERTIES OF MATTER Exercise:Exercise-2 (Concept Applicator)
Explore 28 Videos
- SYSTEM OF PARTICLES & ROTATIONAL MOTION Book:DISHA PUBLICATIONChapter:SYSTEM OF PARTICLES & ROTATIONAL MOTION Exercise:EXERCISE-2 : CONCEPT APPLICATOR
Explore 28 Videos
- THERMODYNAMICS Book:DISHA PUBLICATIONChapter:THERMODYNAMICS Exercise:EXERCISE -2 : CONCEPT APPLICATOR
Explore 29 Videos
Similar Questions
Find the thermal resistance of an aluminium rod of length 20cm and area of cross section 1cm2 . The heat current is along the length of the rod. Thermal conductivity of aluminium =200Wm−1K−1 .
View SolutionHeat is flowing through a rod of length 25.0cm having cross-sectional area 8.80cm2. The coefficient of thermal conductivity for the material of the rod is K=9.2×10−2kcals−1m−1.∘C−1. The Temperatures of the ends of the rod are 125∘C and 0∘C in the steady state. Calculate (i) temeprature gradient in the rod (ii) temperature of a point at a distance of 10.0cm from the hot end and (iii) rate of flow of heat.
View Solution
Knowledge Check
The heat is flowing through a rod of length 50 cm and area of cross-section 5cm2 . Its ends are respectively at 25∘C and 125∘C . The coefficient of thermal conductivity of the material of the rod is 0.092kcal/m×s×.∘C . The temperature gradient in the rod is
A2∘C/cmB2∘C/mC20∘C/mD20∘C/cmTime in which a layer of ice of thickness 10 cm will increase by 5 cm on te surface of a pond when temperature of the surrounding is −10∘C coefficient of thermal conductivity of ice K=0.005(Calcm−sec−.∘C) and density ρ=0.9gram/cm3 (L=80cal/g)
A20 HoursB25 HoursC30 HoursD5 HoursThe ends of copper rod of length 1m and area of cross section 1cm2 are maintained at 0∘C and 100∘C. At the centre of rod, there is a source of heat of 32W. The thermal conductivity of copper is 400W/mK
 AThe temperature of rod at centre is 250∘CBThe temperature of rod at centre is 50∘CCThe temperature gradient in right half is 500∘C/mDThe temperature gradient in left half is 300∘C/m
AThe temperature of rod at centre is 250∘CBThe temperature of rod at centre is 50∘CCThe temperature gradient in right half is 500∘C/mDThe temperature gradient in left half is 300∘C/m
Calculate the rate of loss of heat through a glass window of area 1000cm2 and thickness 0.4 cm when temperature inside is 37∘C and outside is −5∘)C . Coefficient of thermal conductivity of glass is 2.2×10−3cals−1cm−1K−1.
View SolutionFigure shows a steel rod joined to a brass eod. Each of the rods has length of 31cm and area of cross-section 0.20cm2. The junction is maintained at a constant temperature 50∘C and the two ends are maintained at 100∘C. The amount of heat taken out from the cold junction in 10 minutes after the steady state is reached in n×102J. Find 'n' the thermal conductivities are Ksteel=46W/m−∘C and Kbrass=109W/m−∘C.
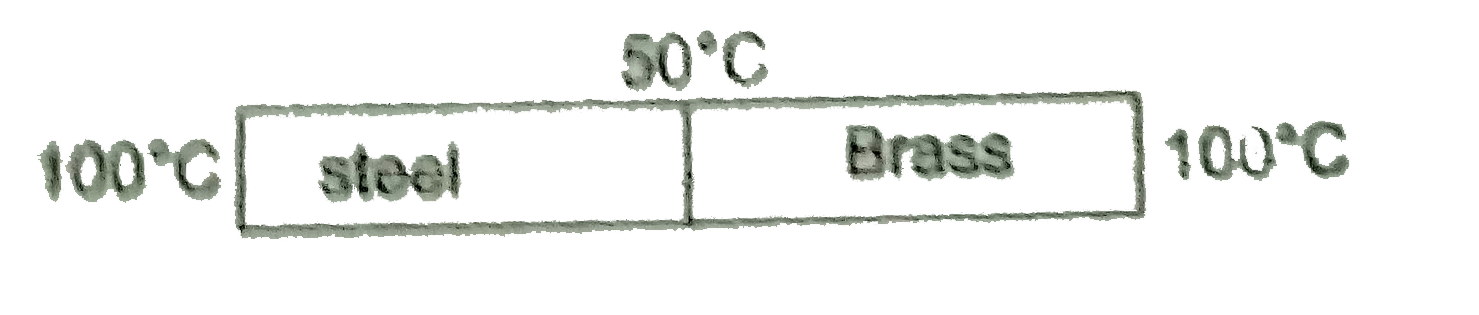
View SolutionFind the thermal resistance of an aluminium rod of length 0.20 m and area of cross section 1×10−4m2. The heat current is along the length of the rod. [Thermal conductivity of aluminium=200Wm−1K−1]
View SolutionA black body at a temperature of 127∘C raidates heat at the rate of 1cal/cm×sec. At a temperature of 527∘C the rate of heat radiation from the body in (cal/cm×sec) will be
View SolutionA black body at a temperature of 227∘C radiates heat energy at the rate of 5 cal/cm-sec. At a temperature of 727∘C, the rate of heat radiated per unit area in cal/cm will be
View Solution

