A sphere of mass 8m collides elastically (in one dimension) with a block of mass 2m. If the initial energy of sphere is E. What is the final energy of sphere?
0.8 E
0.36 E
0.08 E
0.64E
The correct Answer is:B
For elastic collision in one dimension
v1=2m2u2m1+m2+m1−m2u1m1+m2
As mass 2m,is at rest,So u2=0
⇒v1=(8m−2m)u8m+2m=35u
Final energy of sphere =(K.E.)f
12(8m)(3u5)2=12(8m)u2×(35)2=925E.
0.36E
Topper's Solved these Questions
- CONCEPT BUILDERBOOK - DISHA PUBLICATIONCHAPTER - CONCEPT BUILDEREXERCISE - Exercise-1 Concept Builder (Topic 2:Energy)
15 Videos
- CONCEPT BUILDERBOOK - DISHA PUBLICATIONCHAPTER - CONCEPT BUILDEREXERCISE - Exercise-1 Concept Builder (topic 3:Power)
20 Videos
- CONCEPT BUILDERBOOK - DISHA PUBLICATIONCHAPTER - CONCEPT BUILDEREXERCISE - Exercise-2 Concept Applicator
27 Videos
- COMMUNICATION SYSTEM BOOK - DISHA PUBLICATIONCHAPTER - COMMUNICATION SYSTEM EXERCISE - EXERCISE-2 : Concept Applicator
30 Videos
- CURRENT ELECTRICITYBOOK - DISHA PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-2 Concept Applicator
23 Videos
Similar Questions
The spring balance is used to measure the mass of the given sphere. What is the mass of the sphere ?
 .
.
View SolutionA moving body of mass m makes a head on elastic collision with another body of mass 2m which is initially at rest. Find the fraction of kinetic energy lost by the colliding particles after collision.
View Solution
Knowledge Check
A sphere of radius R and mass M collides elastically with a cubical block of mass M and side 2R. The entire system is on a smooth horizontal ground. Given that the sphere was rolling without slipping with an angular velocity ω at the time of collision. The velocities of the sphere and the block after the collision are
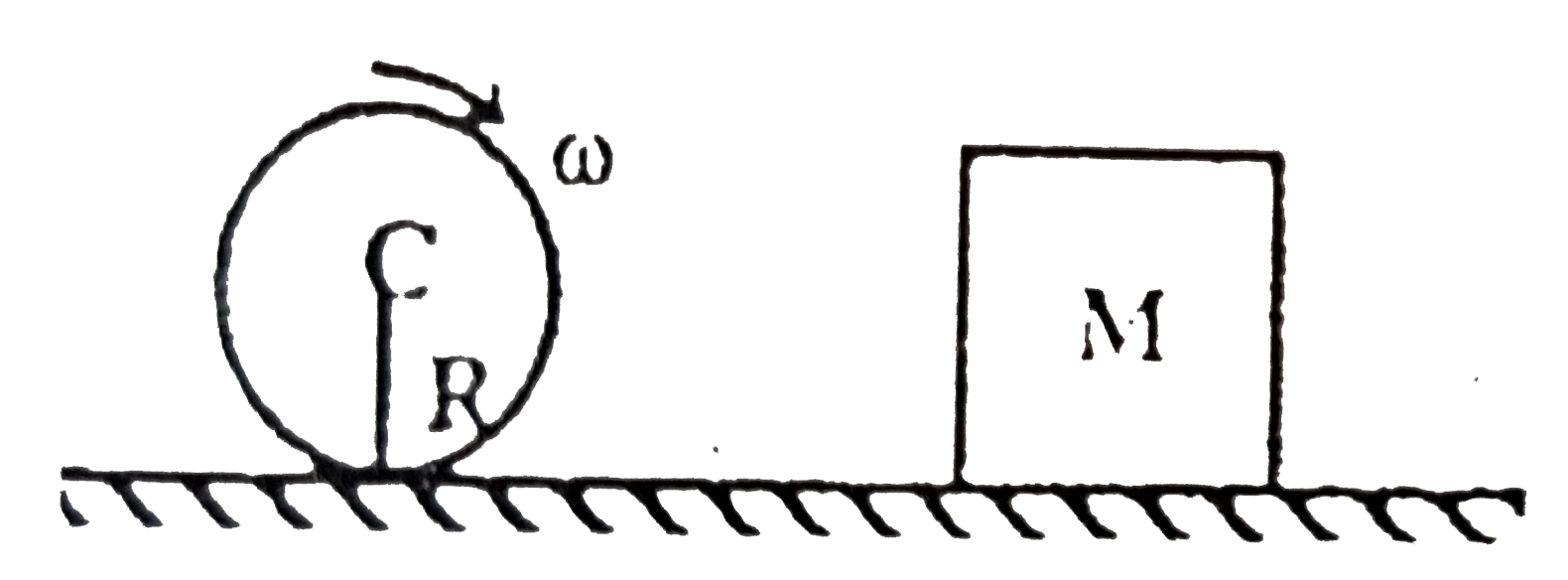 Aωsphere=0, vsphere=0, vblock=vBωsphere=ω, vsphere=0, vblock=vCωsphere=0, vsphere=0, vblock=0Dωsphere=ω2, vsphere=v2, vblock=v2
Aωsphere=0, vsphere=0, vblock=vBωsphere=ω, vsphere=0, vblock=vCωsphere=0, vsphere=0, vblock=0Dωsphere=ω2, vsphere=v2, vblock=v2A body of mass M1 collides elastically with another mass M2 at rest. There is maximum transfer of energy when :
AM1>M2BM1<M2CM1=M2Dsame for all values of M1 and M2If a solid sphere of mass 500 gram rolls without slipping with a velocity of 20 cm/s, then the rolling kinetic energy of the sphere will be
A140 JB280 JC0.014 JD0.028 J
A sphere of mass '2m' gm collides with a stationary sphere of '3m' gm and sticks to it.Then the loss in kinetic energy during collision is
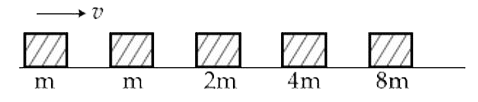
View SolutionBlocks of masses m , 2m , 4m and 8m are arranged in a line on a frictionless floor . Another block of mass m , moving with speed v along the same line (see figure ) collides with mass m in perfectly inelastic manner. All the subsequent collisions are also perfectly inelastic. By the time the last block of mass 8 m starts moving the total energy loss is p% of the original energy . Value of 'p' is close to :
View SolutionA thin hollow sphere of mass m is completely filled with a liquid of mass m. When the sphere rolls with a velocity v kinetic energy of the system is (neglect friction)
View SolutionA body of mass 2 m moving with velocity v makes a head - on elastic collision with another body of mass m which is initially at rest. Loss of kinetic energy of the colliding body (mass 2 m) is
View SolutionA smooth sphere A of mass m collides elastically with an identical sphere B at rest. The velocity of A before collision is 8m/s in a direction making 60∘ with the line of centres at the time of impact.
View Solution
