A vector of magnitude b is rotated through angle $θ$ . What is the change in magnitude of the vector?

A

$2 b sin \frac{θ}{2}$

B

$2 b cos \frac{θ}{2}$

C

$2 b sin θ$

D

$2 b cos θ$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$- - \to P Q + - - \to Q R = - - \to P R$
$∴ - - \to Q R = \to b . - \to b$

Now ${∣ ∣ \to b . - \to b ∣ ∣}^{2} = (\to b . - \to b) . (\to b . - \to b)$
$= b .^{2} - 2 . cos θ + b^{2} = 2 b^{2} (1 - cos θ) [∵ b . = b]$
$\to b . = \to b = \sqrt{2} b \sqrt{1 - cos θ} = \sqrt{2} (\sqrt{2} sin \frac{θ}{2}) = 2 b sin \frac{θ}{2}$

|

Updated on:21/07/2023

Class 12 PHYSICS MOTION IN A PLANE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A vector of magnitude a is turned through angle $θ$ . The magnitude of change in the vector is given by:
A $| 2 a sin θ |$
B $| 2 a sin θ / 2 |$
C $∣ ∣ ∣ \frac{a}{2} sin θ ∣ ∣ ∣$
D $∣ ∣ ∣ \frac{a}{2} sin θ / 2 ∣ ∣ ∣$
Question 2 - Select One
A vector of length $l$ is turned through the angle $θ$ about its tail. What is the change in the position vector of its head ?
A $l cos (θ / 2)$
B $2 l sin (θ / 2)$
C $2 l cos (θ / 2)$
D $l sin (θ / 2)$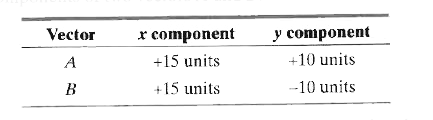
Question 3 - Select One

Determine the magnitude of the vector sum, $A + B .$
A5 units
B15 units
C20 units
D30 units

DISHA PUBLICATION-MOTION IN A PLANE -Exercise -1 : CONCEPT BUILDER (TOPICWISE)

Home
Ask Doubt
Profile