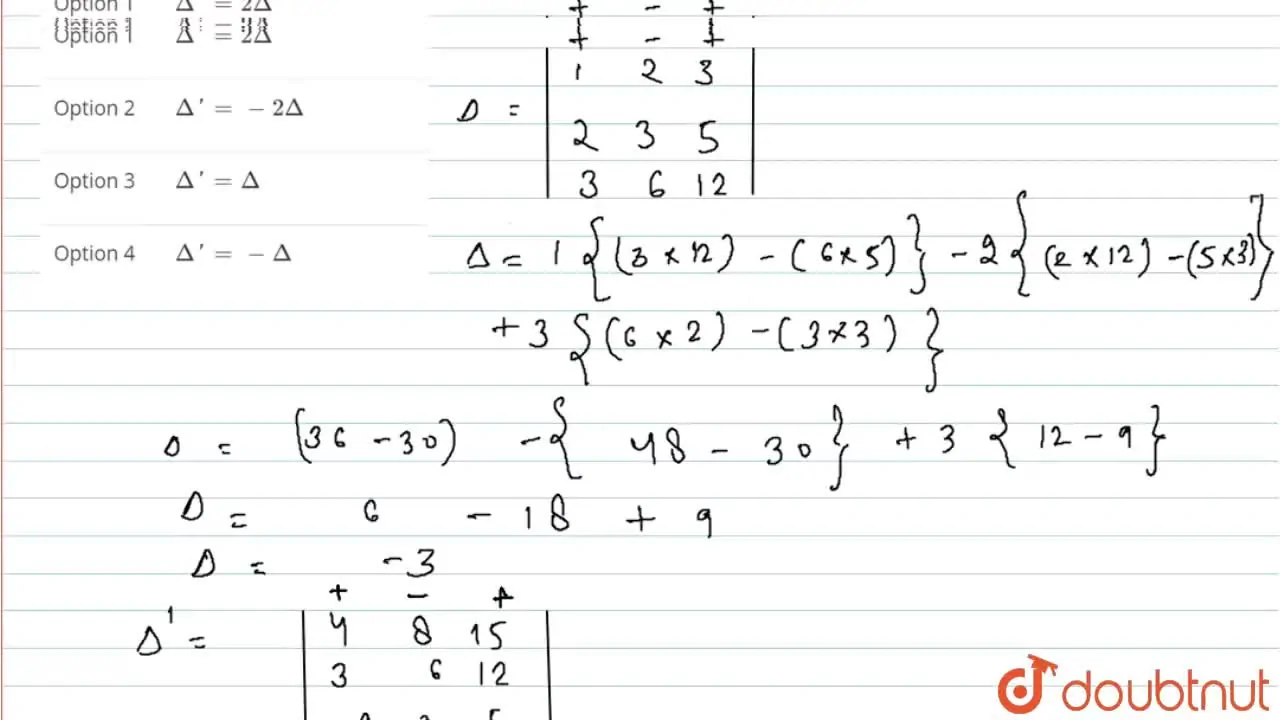If Δ=∣∣ ∣∣1232353612∣∣ ∣∣andΔ'=∣∣ ∣∣48153612235∣∣ ∣∣ , then
Δ'=2Δ
Δ'=−2Δ
Δ'=Δ
Δ'=−Δ
The correct Answer is:D
Step by step video, text & image solution for If Delta = |{:(1,2,3),(2,3,5),(3,6,12):}|and Delta' = |{:(4,8,15),(3,6,12),(2,3,5):}| , then by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - DISHA PUBLICATIONCHAPTER - DETERMINANTSEXERCISE - EXERCISE -2 CONCEPT APPLICATOR30videos
DETERMINANTS
- BOOK - DISHA PUBLICATIONCHAPTER - DETERMINANTSEXERCISE - EXERCISE -2 CONCEPT APPLICATOR30videos
DETERMINANTS
- BOOK - DISHA PUBLICATIONCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise-2 : Concept Applicator30videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - DISHA PUBLICATIONCHAPTER - DIFFERENTIAL EQUATIONS EXERCISE - Exercise-2 : Concept Applicator30videos
DIFFERENTIAL EQUATIONS
Similar Questions
If A[123564−12−31]andB=⎡⎢ ⎢ ⎢ ⎢ ⎢ ⎢⎣5321−354112⎤⎥ ⎥ ⎥ ⎥ ⎥ ⎥⎦, then find AB and BA.
View SolutionEvaluate Δ=∣∣ ∣∣345−62−3817∣∣ ∣∣
View SolutionIf A⎛⎜⎝1343−15−24−3⎞⎟⎠=⎛⎜⎝3−15134+4−86⎞⎟⎠, then A=
View SolutionIf Δ=∣∣ ∣∣−12+3i5−4i2−3i81−i5+4i1+i3∣∣ ∣∣ then Δ is
View SolutionifA=[12−5−346]andB[−23−4123]' then find 2A+B.
View SolutionIf A=[2356−12−34]andB=[4−5378−3−12], then find AT+BTand(A+B)T. What do you notice ?
View SolutionΔ=∣∣ ∣∣538201123∣∣ ∣∣=
View SolutionIf ,A =[12−24],then -3A=[−3−66−12]
View SolutionIf Δ=∣∣ ∣∣538604123∣∣ ∣∣ then the minor of the element a21 is
View SolutionFind the inverses of the following matrices by adjoint method :
(1)(1223) (2)(5432) (3)(3−268) (4)(2−335).View Solution