Consider te following
I. New Delhi is in Nepal.
II. Every relation is a function. III. Do your homework.
Choose the correct option.
I and II are statements.
I and III are statements.
II and III are statements.
I,II and III are statements.
The correct Answer is:A
To solve the given question, we need to analyze each of the three sentences provided and determine whether they qualify as statements based on the definition of a statement in mathematical reasoning.
1. Identify the Definition of a Statement:
A statement is defined as a declarative sentence that can be classified as either true or false, but not both.
2. Analyze Sentence I: "New Delhi is in Nepal.":
- This sentence can be evaluated for its truth value.
- The statement is actually false because New Delhi is the capital of India, not Nepal.
- Since it can be classified as false, it qualifies as a statement.
3. Analyze Sentence II: "Every relation is a function.":
- This sentence can also be evaluated for its truth value.
- This statement is false because not all relations are functions; a function must have a unique output for each input.
- Since it can be classified as false, it qualifies as a statement.
4. Analyze Sentence III: "Do your homework.":
- This sentence is an imperative or command.
- It does not have a truth value; it cannot be classified as true or false.
- Therefore, it does not qualify as a statement.
5. Conclusion:
- From the analysis, we find that:
- Sentence I is a statement (false).
- Sentence II is a statement (false).
- Sentence III is not a statement.
- Thus, the correct option is that only the first two sentences are statements.
Final Answer:
The correct option is that only the first two sentences (I and II) are statements.
---
A statement is defined as a declarative sentence that can be classified as either true or false, but not both.
- This sentence can be evaluated for its truth value.
- The statement is actually false because New Delhi is the capital of India, not Nepal.
- Since it can be classified as false, it qualifies as a statement.
- This sentence can also be evaluated for its truth value.
- This statement is false because not all relations are functions; a function must have a unique output for each input.
- Since it can be classified as false, it qualifies as a statement.
- This sentence is an imperative or command.
- It does not have a truth value; it cannot be classified as true or false.
- Therefore, it does not qualify as a statement.
- From the analysis, we find that:
- Sentence I is a statement (false).
- Sentence II is a statement (false).
- Sentence III is not a statement.
- Thus, the correct option is that only the first two sentences are statements.
The correct option is that only the first two sentences (I and II) are statements.
Topper's Solved these Questions
- MATHEMATICAL REASONINGBook:DISHA PUBLICATIONChapter:MATHEMATICAL REASONINGExercise:Exercise-2 : Concept Applicator
Explore 30 Videos
- MATHEMATICAL REASONINGBook:DISHA PUBLICATIONChapter:MATHEMATICAL REASONINGExercise:Exercise-2 : Concept Applicator
Explore 30 Videos
- LINEAR INEQUALITIESBook:DISHA PUBLICATIONChapter:LINEAR INEQUALITIESExercise:Exercise -2 : Concept Applicator
Explore 30 Videos
- MATRICESBook:DISHA PUBLICATIONChapter:MATRICESExercise:Exercise 2: Concept Applicator
Explore 30 Videos
Similar Questions
Knowledge Check
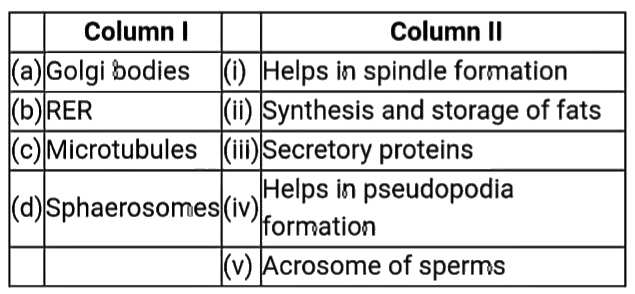
Match the columns I, II and III. Choose the correct option.
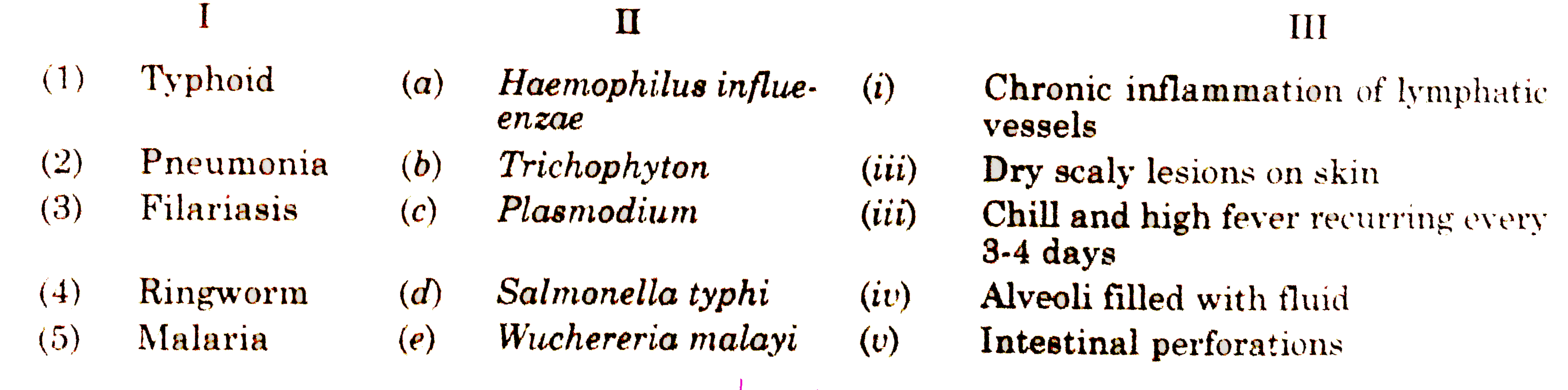 A1-a-I,2-c-ii,3-b-iii,4-e-v,5-d-ivB1-d-I,2-e-ii,3-b-iii,4-c-v,5-d-ivC1-b-I,2-c-ii,c-e-iii,4-a-v,5-d-ivD1-d-v,2-a-iv,3-e-I,5-d-iii
A1-a-I,2-c-ii,3-b-iii,4-e-v,5-d-ivB1-d-I,2-e-ii,3-b-iii,4-c-v,5-d-ivC1-b-I,2-c-ii,c-e-iii,4-a-v,5-d-ivD1-d-v,2-a-iv,3-e-I,5-d-iiiMatch the I with column II and choose the correct option.
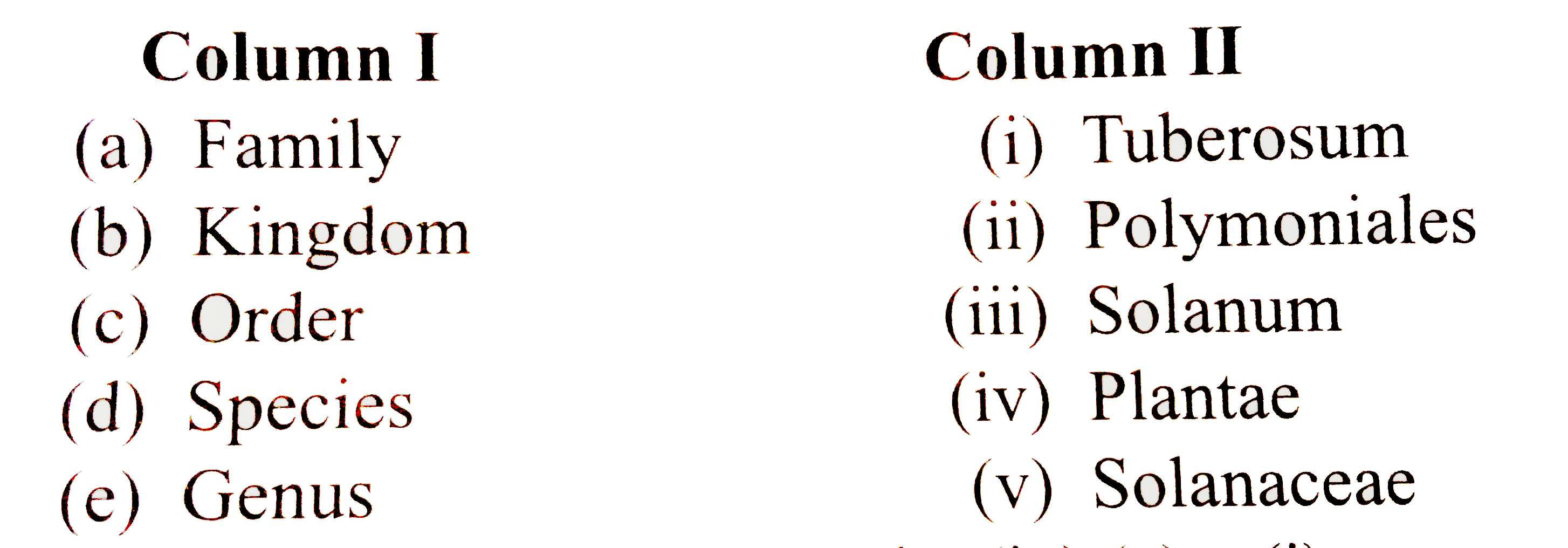 Aa-iv,b-iii,c-v,d-iv,e-iBa-v,b-iv,c-ii,d-I,e-iiiCa-iv,b-v,c-ii,d-I,e-iiiDa-v,b-iiic-ii,d-I,e-iv
Aa-iv,b-iii,c-v,d-iv,e-iBa-v,b-iv,c-ii,d-I,e-iiiCa-iv,b-v,c-ii,d-I,e-iiiDa-v,b-iiic-ii,d-I,e-ivMatch the enzyme in column I with its function in column II and choose the correct option.
 AABCD2143BABCD3412CABCD2443DABCD1243
AABCD2143BABCD3412CABCD2443DABCD1243
Consider the following arrangement and choose the correct options
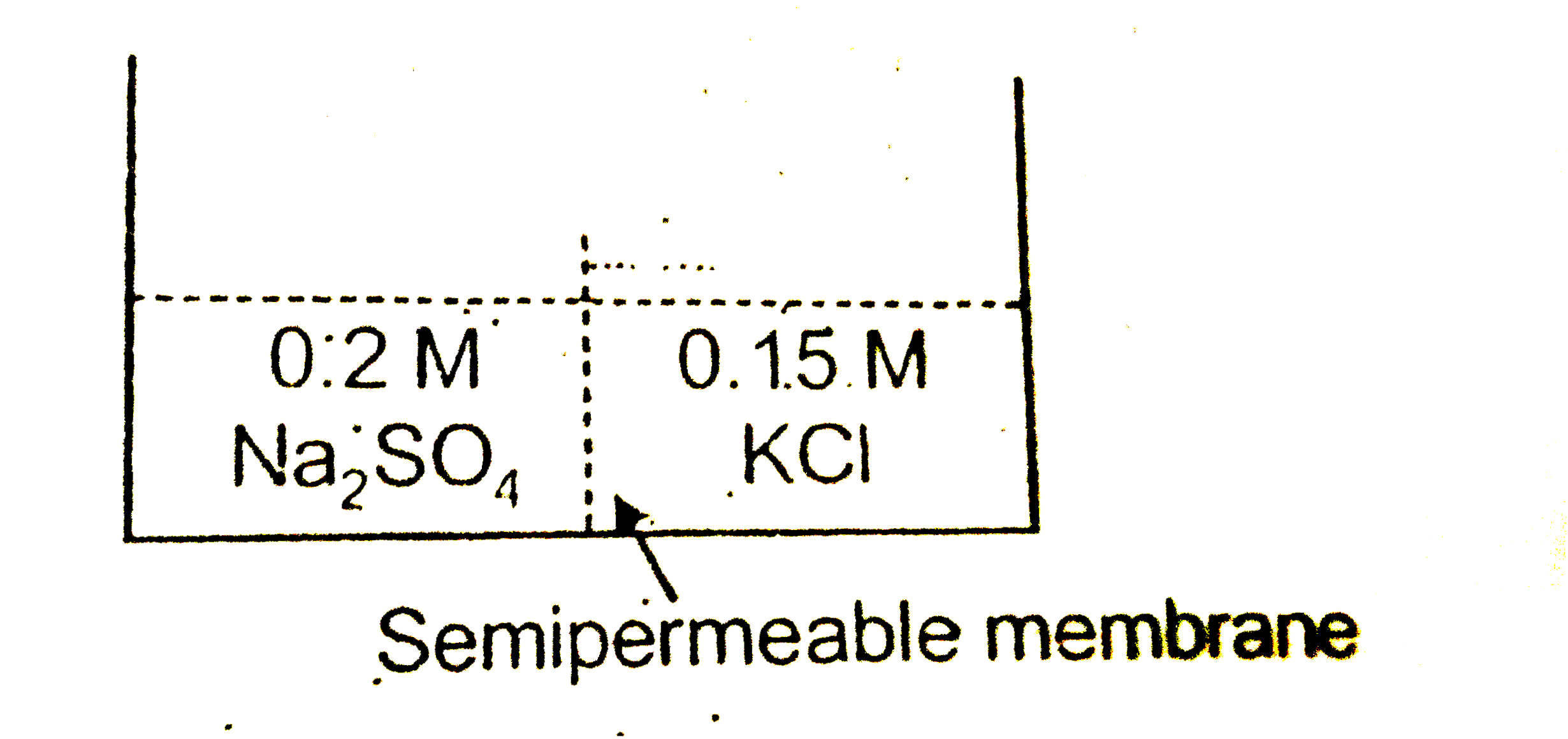
View SolutionConsider the following statements
I Distillation is very careful for low boiling metals like Zn and Hg
II
Choose the correct option
View SolutionConsider the following statement
I. "Every rectangle is a square" is a statement.
II. "Close the door" is not a statement.
Choose the correct option.
View SolutionMendelism was rediscovered by
I. Morgan
II. De Vries
III. Correns
IV. Tschermak
Choose the correct option
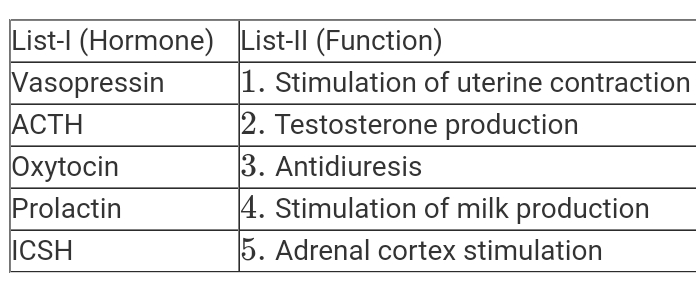
View SolutionMatch the hormone of in the List I with function in the List-II and choose the correct option .
View Solution