Let f:R→(0,1) be a continuous function. Then, which of the following function (s) has (have) the value zero at some point in the interval (0,1)?
ex−∫x0π⋅2−xf(t)sin t dt
f(x)+∫π20f(t)sint dt
x−∫0f(t)cos t dt
x9−f(x)
The correct Answer is:C, D
∵ex∈(1,e) in (0,1)and∫x0f(t)sint dt ∈(0,1)
∴ex−∫x0f(t)sin t dit cannot be zero.
So , option (a) is incorrect.
(b) f(x)+∫π20f(t)sin t dt always positive
∴ Option (b) is incorrect.
( c) Let h (x) =x−∫π2−x0f(t)cost dt
h(0)=−∫π20f(t)cos t dt <0
h(1)=1−∫π2−10f(t)cos t dt <0
∴ Option ( c) is correct.
(d) Let g (x) =x9−f(x)
g(0)=−f(0)<0
g(1)=1−f(1)<0
∴ Option (d) is correct .
Topper's Solved these Questions
- DEFINITE INTEGRATIONBook:IIT JEE PREVIOUS YEARChapter:DEFINITE INTEGRATIONExercise:PERIODICITY OF INTEGRAL FUNCTIONS
Explore 6 Videos
- DEFINITE INTEGRATIONBook:IIT JEE PREVIOUS YEARChapter:DEFINITE INTEGRATIONExercise:ESTIMATION, GAMMA FUNCTION AND DERIVATIVE OF INDEFINITE INTEGRAL
Explore 22 Videos
- COMPLEX NUMBERSBook:IIT JEE PREVIOUS YEARChapter:COMPLEX NUMBERSExercise:TOPIC 5 DE-MOIVRES THEOREM,CUBE ROOTS AND nth ROOTS OF UNITY (INTEGER ANSWER TYPE QUESTION)
Explore 1 Video
- DIFFERENTIAL EQUATIONS Book:IIT JEE PREVIOUS YEARChapter:DIFFERENTIAL EQUATIONS Exercise:TOPIC 3 APPLICATIONS OF HOMOGENEOUS DIFFERENTIAL EQUATIONS <br> ANALYTICAL & DESCRIPTIVE QUESTIONS
Explore 7 Videos
Similar Questions
Let f:R→(0,1) be a continuous function. Then, which of the following function (s) has (have) the value zero at some point in the interval (0,1)? ex−∫x0f(t)sintdt (b) f(x)+∫π20f(t)sintdt(c) x−∫π2−x0f(t)costdt (d) x9−f(x)
View SolutionLet f:[0,1]→[0,1] be a continuous function. Then prove that f(x)=x for at least one 0≤x≤1.
View Solution
Knowledge Check
Which of the following graphs represent function whose derivatives have a maximum in the interval (0,1) ?
A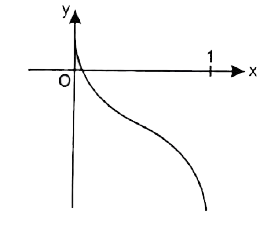 B
B C
C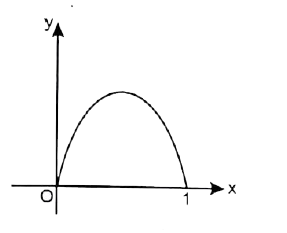 D
D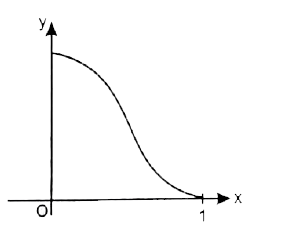
Which of the following graphs represent function whose derivatives have a maximum in the interval (0,1) ?
A B
B C
C D
D
Let f(x) be a continuous function on R and f(0)=f(2), then the equation f(x)=f(x+1) will have :-
Aat least one root in [0,1]Bat most one root in [0,1]Cexactly one root in [0,1]Dno root in [0,1]
Let f:[0,1]→[0,1]be a continuous function such that f(f(x))=1forallx∈[0,1]then:
View SolutionVerify Lagrange's Mean Value theorem for the following functions in the given intervals
f(x) = ex in the interval [0,1].
View SolutionThe points at which the function, f(x)=|x-0.5|+|x-1|+tanx does not have a derivative in the interval (0,2) are
View SolutionVerify Lagrange's Mean Value theorem for the following functions in the given intervals
f(x) = tan−1x in the interval [0,1]
View SolutionLet f,g:[−1,2]→ be continuous functions which are twice differentiable on the interval (-1,2). Let the values of f and g at the points and 2 be as given in the following table:

In each of the intervals (-1,0) and (0, 2) the function (f-3g) never vanishes. Then the correct statements(s) is(are) :
View Solution
