Question

Let $i={\int }_a^b(x^4-2x^2)dx$ for $(a,b)$ which given integration is minimum $(b>0)$ (a) $(\sqrt{2},-\sqrt{2})$ (b) $(0,\sqrt{2})$ (c) $(-\sqrt{2},\sqrt{2})$ (d) $(\sqrt{2},0)$

Options

A. `(-sqrt(2),0)`
B. `(0,sqrt(2))`
C. `(sqrt(2),-sqrt(2))`
D. `(-sqrt(2),sqrt(2))`

Answer

D

Explanation

We have , I `=int_(a)^(b)(x^(4)-2x^(2))dx`
Let `f(x)=x^(4)-2x^(2)=x^(2)(x^(2)-2)`
` =x^(2)(x-sqrt(2))(x+sqrt(2))`
Graph ` y=f(x)=x^(4)-2x^(2)` is

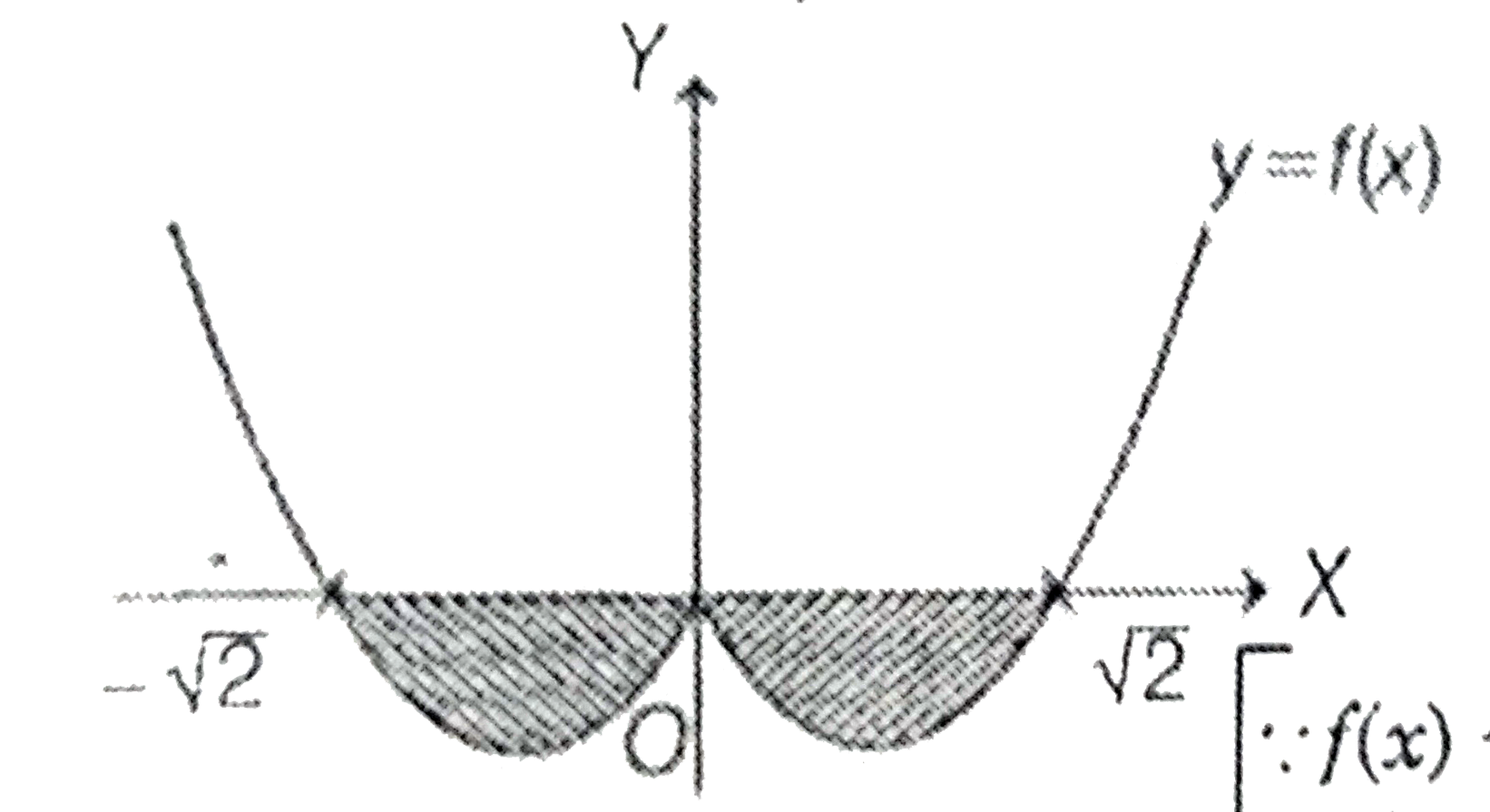
Note that the definite integral `int_(a)^(b)(x^(4)-2x^(2)) dx` represent the area bounded by ` y= f(x),x =` a , b and the X - axis.
But between `x=-sqrt(2)andx=sqrt(2),f(x)` lies below the X - axis and so value definite integral will be negative. Also , as long as f(x) lie below the X - axis , the value of definite integral will be minimum.
`:.(a.b)=(-sqrt(2),sqrt(2)` for minimum of I.