A student scores the following marks in five tests 45, 54, 41, 57, 43. His score is not known for the sixth test. If the mean score is 48 in the six tests, then the standard deviation of the marks in six tests is
103
10√3
100√3
1003
The correct Answer is:B
To solve the problem step by step, we need to find the standard deviation of the marks obtained by the student in six tests, given that the mean score is 48.
Step 1: Calculate the total marks needed for six tests
Given that the mean score for six tests is 48, we can use the formula for mean:
Mean=Total Marksn
Where n is the number of tests (which is 6). Therefore, the total marks for six tests can be calculated as:
Total Marks=Mean×n=48×6=288
Step 2: Calculate the sum of the marks from the first five tests
The marks obtained in the first five tests are:
- Test 1: 45
- Test 2: 54
- Test 3: 41
- Test 4: 57
- Test 5: 43
Now, we calculate the sum of these marks:
Sum of first five tests=45+54+41+57+43=240
Step 3: Find the score in the sixth test
Let x be the score in the sixth test. According to our earlier calculation, the total marks for six tests is 288. Therefore, we can write:
240+x=288
Solving for x:
x=288−240=48
Step 4: List all the marks
Now we have all the marks:
- Test 1: 45
- Test 2: 54
- Test 3: 41
- Test 4: 57
- Test 5: 43
- Test 6: 48
Step 5: Calculate the mean (already known)
The mean of these six tests is given as 48, which we have confirmed.
Step 6: Calculate the standard deviation
The formula for standard deviation (SD) is:
SD=√∑(xi−¯x)2n
Where:
- xi are the individual test scores,
- ¯x is the mean,
- n is the number of tests.
Calculating (xi−¯x)2 for each score:
1. (45−48)2=(−3)2=9
2. (54−48)2=(6)2=36
3. (41−48)2=(−7)2=49
4. (57−48)2=(9)2=81
5. (43−48)2=(−5)2=25
6. (48−48)2=(0)2=0
Now, summing these squared differences:
∑(xi−¯x)2=9+36+49+81+25+0=200
Step 7: Calculate the standard deviation
Now, substituting back into the SD formula:
SD=√2006=√1003=10√3≈5.77
Final Answer
The standard deviation of the marks in the six tests is 10√3.
---
Given that the mean score for six tests is 48, we can use the formula for mean:
The marks obtained in the first five tests are:
- Test 2: 54
- Test 3: 41
- Test 4: 57
- Test 5: 43
Let x be the score in the sixth test. According to our earlier calculation, the total marks for six tests is 288. Therefore, we can write:
Now we have all the marks:
- Test 2: 54
- Test 3: 41
- Test 4: 57
- Test 5: 43
- Test 6: 48
The mean of these six tests is given as 48, which we have confirmed.
The formula for standard deviation (SD) is:
- xi are the individual test scores,
- ¯x is the mean,
- n is the number of tests.
2. (54−48)2=(6)2=36
3. (41−48)2=(−7)2=49
4. (57−48)2=(9)2=81
5. (43−48)2=(−5)2=25
6. (48−48)2=(0)2=0
Now, substituting back into the SD formula:
The standard deviation of the marks in the six tests is 10√3.
Topper's Solved these Questions
- MISCELLANEOUSBOOK - IIT JEE PREVIOUS YEARCHAPTER - MISCELLANEOUSEXERCISE - MISCELLANEOUS
87 Videos
- MATRICES AND DETERMINANTSBOOK - IIT JEE PREVIOUS YEARCHAPTER - MATRICES AND DETERMINANTSEXERCISE - SOLVING SYSTEM OF EQUATIONS (INTEGER ANSWER TYPE QUESTION)
2 Videos
- PARABOLABOOK - IIT JEE PREVIOUS YEARCHAPTER - PARABOLAEXERCISE - TOPIC 4 DIAMETER, CHORD OF CONTACT, CHORD BISECTED AND PRODUCT OF PAIR OF TANGENTS OBJECTIVES QUESTION II (ANALYTICAL & DESCRIPTIVE )
5 Videos
Similar Questions
There are 60 students in a class. The following is the frequency distribution of the marks obtained by the students in a test:

Where "p" is positive integer. Determine the mean and standard deviation of the marks.
View SolutionCalculate the mean of the scores of 20 students in a mathematics test
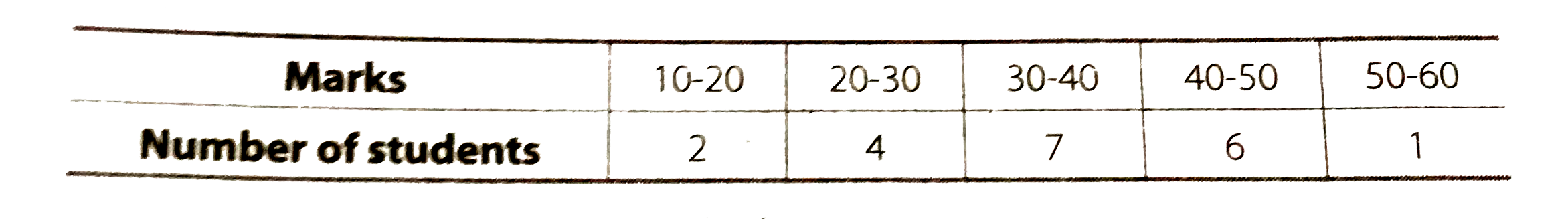
View Solution
Knowledge Check
The marks of a student in 6 tests are 41,45,54,57,43 and x. If the mean marks of these tests is 48. then standard deviation of these tests is
A10√3B10√2C103D203Find the mode of the following frequency table, which gives the marks scored by 40 students in a test:
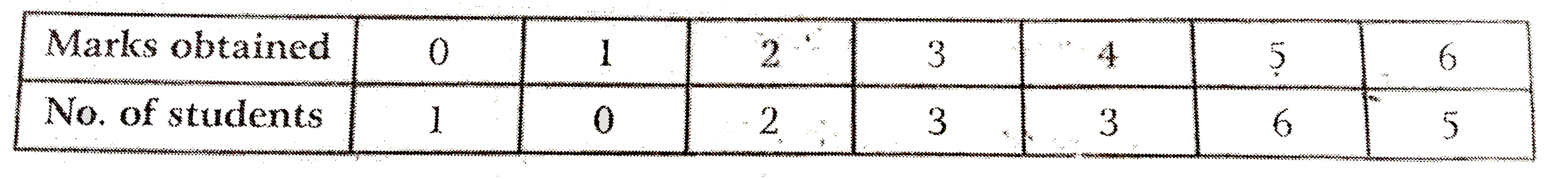 A5B6C3D4
A5B6C3D4If the standard deviation for the marks obtained by a student in monthly tests is 36 then the variance is
A6B36C1296Dnone of these
The marks scored by Rohit in two tests were 65 and 70. Find the minimum marks the should score in the third test to have an average of at least 65 marks.
View SolutionWho has scored the most Test hundreds ever?
View SolutionWho has scored the slowest century in the test cricket?
View SolutionIn a test Arun scored 20 % and failed by 10 marks Bala scored 40% in the same test and obtained 10 marks more than the pass mark. Find the maximum marks.
View SolutionIn a norm referenced test, a student's score is interpreted, by comparing it
View Solution